编号为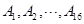
的16名篮球运动员在某次训练比赛中的得分记录如下：
| 运动员编号 |
 |
 |
 |
 |
 |
 |
 |
 |
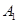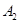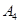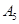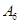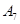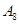| 得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
| 运动员编号 |
 |
 |
 |
 |
 |
 |
 |
 |
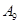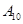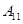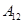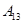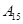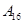| 得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
（Ⅰ）将得分在对应区间内的人数填入相应的空格；
| 区间 |
 |
 |
 |
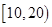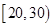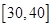| 人数 |
|
|
|
（Ⅱ）从得分在区间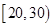内的运动员中随机抽取2人，
（i）用运动员的编号列出所有可能的抽取结果；
（ii）求这2人得分之和大于50的概率．
是R上的函数，且满足
并且对任意的实数
都有
，求
，试求
的最大值.
，求函数
的解析式.
=
+
（t为实数）；
的一支上有不同的三点
，它们与点
的距离
依次成等差数列。
的值；
的垂直平分线经过某一定点，并求出定点的坐标。