(本小题13分)设命题P:复数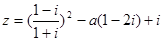 对应的点在第二象限;
对应的点在第二象限;
命题q:不等式 对于
对于 恒成立;
恒成立;
如果“p且q”为假命题,“p或q”为真命题,求实数a的取值范围。
(本小题满分13分)已知抛物线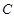 的顶点为坐标原点,焦点为
的顶点为坐标原点,焦点为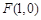 ,
,
(Ⅰ)求抛物线的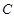 方程;
方程;
(Ⅱ)设是抛物线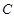 上的点,且满足
上的点,且满足 ,当
,当 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点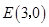 时,求
时,求 的面积.
的面积.
(本小题满分12分)已知 为正数数列的前
为正数数列的前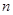 项和,称
项和,称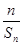 是正数数列的前
是正数数列的前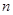 项“平均倒数”.若已知正数数列的前项的“平均倒数”为,且.
项“平均倒数”.若已知正数数列的前项的“平均倒数”为,且.
(Ⅰ)求 的值;
的值;
(Ⅱ)若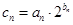 ,其中
,其中 为正数数列
为正数数列 的前
的前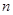 项和,证明:
项和,证明: .
.
(本小题满分12分)某中学准备在“植树节”来临之际,组织学生进行植树活动,学校学生会对一批花苗的高度(单位:cm),进行抽样检测,检测结果的频率分布直方图如图所示.根据标准, 花苗高度在区间[20,25)上的为一等品, 在区间[15,20)和区间[25,30)上的为二等品, 在区间[10,15)和[30,35)上的为三等品.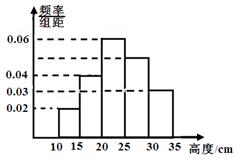
(Ⅰ)用频率估计概率, 现从该批花苗中随机抽取一株, 求其为二等品的概率;
(Ⅱ)已知检测结果为一等品的有6株,现随机从三等品中有放回地连续取两次,每次取1株,求取出的两株花苗中恰有1件的长度在区间[30,35)上的概率.
(本小题满分12分)如图,在四棱锥中,底面是正方形,底面,, 点 分别是
分别是 的中点,,且交于点.
的中点,,且交于点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面⊥平面;
(本题满分12分)已知
(Ⅰ)求函数的最小正周期;
(Ⅱ)当时,方程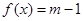 有实数解,求实数的取值范围.
有实数解,求实数的取值范围.