2014年岁末,中国多个省市出现了持续浓重的雾霾天气,截至3月底,今年主城已收获68个
蓝天,三大主要污染物PM10、二氧化硫、二氧化氮明显好转,这与各化工厂积极响应节能减排的号召分不
开.我市某化工厂从2011年就开始控制二氧化硫的排放.图1、图2分别是该厂2011-2014年二氧化硫排
放量(单位:吨)的两幅不完整的统计图,根据图中信息回答下列问题.
(1)该厂2011-2014年二氧化硫排放总量是_____吨,2011年二氧化硫的排放量对应扇形的圆心角是 度,2014年二氧化硫的排放量占这四年排放总量的百分比是 .并补全条形统计图.
(2)为了进一步加大环保宣传力度,重庆市环保局于年底将举行主题为“弘扬环境文化,建设绿色家园”的环保知识竞赛.该化工厂准备从刚分来的4名大学生(其中3名男生,1名女生)中选派2名员工参加比赛,请用列表法或画树状图的方法,求出所选两位参赛选手恰好是一男一女的概率.
已知:如图,在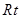 △
△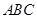 中,∠
中,∠ ,
,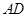 平分∠
平分∠ ,
, ,垂足为点
,垂足为点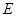 ,
,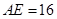 ,
, .求:
.求: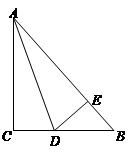
(1)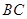 的长;
的长;
(2)求∠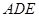 的正切值.
的正切值.
解方程组: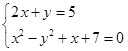 .
.
如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动. 当Q点到达B点时,动点P、Q同时停止运动. 设点P、Q同时出发,并运动了t秒,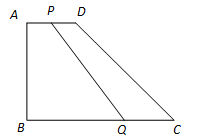
(1)直角梯形ABCD的面积为cm2.
(2)当t= 秒时,四边形PQCD成为平行四边形?
(3)当t= 秒时,AQ=DC;
(4)是否存在t,使得P点在线段DC上且PQ⊥DC?
若存在,求出此时t的值,若不存在,说明理由.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点.
(1)试说明四边形AECG是平行四边形;
(2)若矩形的一边AB的长为3cm,当BC的长为多少时,四边形AECG是菱形?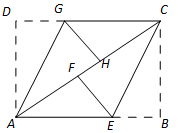
如图,在△ABC中,AB=BC,若将△ABC沿AB方向平移线段AB的长得到△BDE.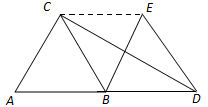
(1)试判断四边形BDEC的形状,并说明理由;
(2)试说明AC与CD垂直.