在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN
90°．
（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；
（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°<α<45°）．
①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；
②如图2，在旋转过程中，当∠DOM15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；
③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD3BP时，猜想此时PE与PF的数量关系，并给出证明；当BDm·BP时，请直接写出PE与PF的数量关系．
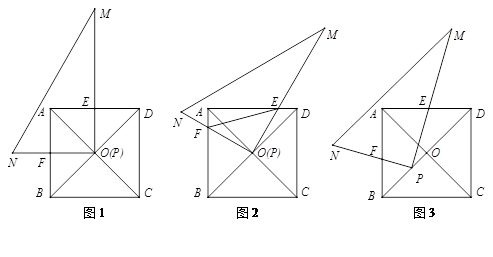
在数轴上把下列各数表示出来，并用“＜”连接各数．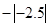
，
，
，
，
．
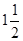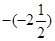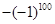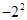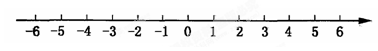
如图，AC⊥BC，AD⊥BD，AD=BC，CE⊥AB，DF⊥AB垂足分别是E、F，求证：CE=DF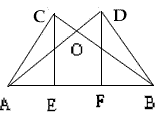
如图，已知AD平分∠BAC交BC于D，DE⊥AB，DF⊥AC，垂足分别是E、F，求证：AD垂直平分EF．
作图题：
（1）利用网格线作图（充分利用格线或格点，完成如下操作）：在BC上找一点P，使点P到AB和AC的距离相等．然后，在射线AP上找一点Q，使QB＝QC
（2）如图，等边△ABC，AD是BC边上的中线，M是AD上的动点，E是AC边上一点
①作点E关于直线AD的对称点点E′；
②当EM+CM的值最小时，作出此时点M的位置（标注为M′）
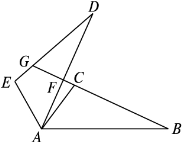
如图，△ABC≌△ADE，且∠CAD＝10°，∠B＝∠D＝25°，∠EAB＝120°，求∠DFB和∠DGB的度数．