某班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况,八年级300名同学零花钱的最主要用途情况,九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.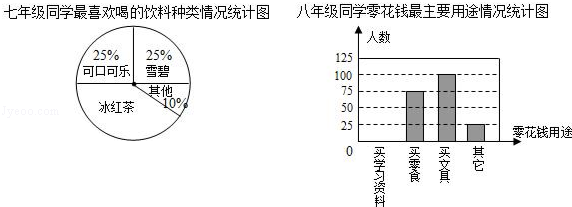
九年级300名同学完成家庭作业时间情况统计图
| 时间 |
1小时左右 |
1.5小时左右 |
2小时左右 |
2.5小时左右 |
| 人数 |
50 |
80 |
120 |
50 |
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少;
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时?(结果保留一位小数)
如图,点 , , , 在一条直线上, , , .求证: .

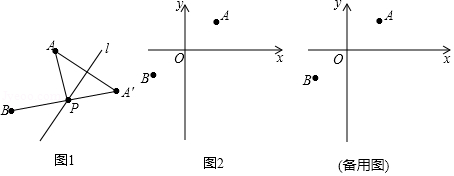
【定义】如图1, , 为直线 同侧的两点,过点 作直线 的对称点 ,连接 交直线 于点 ,连接 ,则称点 为点 , 关于直线 的“等角点”.
【运用】如图2,在平面直角坐标系 中,已知 , 两点.
(1) , , 三点中,点 是点 , 关于直线 的等角点;
(2)若直线 垂直于 轴,点 是点 , 关于直线 的等角点,其中 , ,求证: ;
(3)若点 是点 , 关于直线 的等角点,且点 位于直线 的右下方,当 时,求 的取值范围(直接写出结果).
如图,正方形 中, , 是 边的中点,点 是正方形内一动点, ,连接 ,将线段 绕点 逆时针旋转 得 ,连接 , .

(1)求证: ;
(2)若 , , 三点共线,连接 ,求线段 的长.
(3)求线段 长的最小值.
在平面直角坐标系 中,已知抛物线 为常数).
(1)若抛物线经过点 ,求 的值;
(2)若抛物线经过点 和点 ,且 ,求 的取值范围;
(3)若将抛物线向右平移1个单位长度得到新抛物线,当 时,新抛物线对应的函数有最小值 ,求 的值.
小明购买 , 两种商品,每次购买同一种商品的单价相同,具体信息如下表:
|
次数 |
购买数量(件 |
购买总费用(元 |
|
|
|
|
||
|
第一次 |
2 |
1 |
55 |
|
第二次 |
1 |
3 |
65 |
根据以上信息解答下列问题:
(1)求 , 两种商品的单价;
(2)若第三次购买这两种商品共12件,且 种商品的数量不少于 种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.