、
两座城市之间有一条高速公路，甲、乙两辆汽车同时分别从这条路两端的入口处驶入，并始终在高速公路上正常行驶．甲车驶往城，乙车驶往城，甲车在行驶过程中速度始终不变．甲车距城高速公路入口处的距离
（千米）与行驶时间
（时）之间的关系如图．
（1）求关于的表达式；
（2）已知乙车以60千米/时的速度匀速行驶，设行驶过 程中，相遇前两车相距的路程为
（千米）．请直接写出关于的表达式；
（3）当乙车按（2）中的状态行驶与甲车相遇后，速度随即改为
（千米/时）并保持匀速行驶，结果比甲车晚40分钟到达终点，求乙车变化后的速度．并在图中画出乙车离开城高速公路入口处的距离（千米）与行驶时间（时）之间的函数图象．
如图，已知A（0，4），点B在第三象限，且∠B=300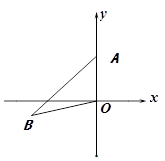
（1）尺规作图：作出△ABO的外接圆⊙P（不写作法，保留作图痕迹）
（2）求点P的坐标．
已知关于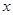
的方程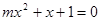
，
（1）当该方程有一根为1时，试确定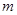
的值
（2）当该方程有两个不相等的实数根时，试确定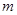的取值范围
先化简，再求值：
，其中
满足x2-2x-4=0
解方程：
（1）4x2－2x－1="0"
（2）
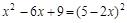
如图，在Rt△ABC中，AC＝4cm，BC＝3cm，点P由B出发沿BA的方向向点A匀速运动，速度为1cm/s，同时点Q由A出发沿AC的方向向点C匀速运动，速度为2cm/s，连接PQ，设运动的时间为t（s），其中0＜t＜2，解答下列问题：
（1）当t为何值时，以P、Q、A为顶点的三角形与△ABC相似？
（2）是否存在某一时刻t，线段PQ将△ABC的面积分成1：2两部分？若存在，求出此时的t，若不存在，请说明理由；
（3）点P、Q在运动的过程中，△CPQ能否成为等腰三角形？若能，请求出此时t的值，若不存在，请说明理由．