(本题满分14分)
已知函数 ,
,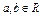 ,
,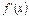 是函数
是函数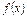 的导函数.
的导函数.
(I)若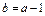 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(II)若 ,
,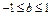 ,求方程
,求方程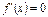 有实数根的概率.
有实数根的概率.
(本小题满分14分)
如图所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=8,AC= ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点, ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B—CE—F的正弦值
(本小题满分12分)
在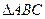 中,角
中,角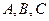 所对应的边分别为
所对应的边分别为 ,且满足
,且满足 .
.
(I)求角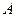 的度数;
的度数;
(II)求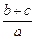 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 的图象过点
的图象过点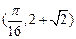
(Ⅰ)求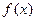 的解析式;
的解析式;
(Ⅱ)写出函数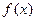 的图象是由函数
的图象是由函数 的图象经过怎样的变换得到的。
的图象经过怎样的变换得到的。
(本小题满分14分) 已知数列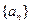 和
和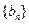 满足:
满足: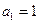 ,
,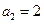 ,
,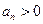 ,
,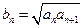 (
(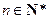 ),且
),且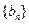 是以
是以 为公比的等比数列.
为公比的等比数列.
(Ⅰ)证明: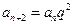 ;
;
(Ⅱ)若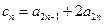 ,证明:数列
,证明:数列 是等比数列;
是等比数列;
(Ⅲ)(理科做,文科不做)若 ,求和:
,求和: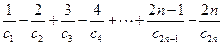 .
.