(本小题满分14分)某地拟建一座长为 米的大桥
米的大桥 ,假设桥墩等距离分布,经设计部门测算,两端桥墩
,假设桥墩等距离分布,经设计部门测算,两端桥墩 、
、 造价总共为
造价总共为 万元,当相邻两个桥墩的距离为
万元,当相邻两个桥墩的距离为 米时(其中
米时(其中 ),中间每个桥墩的平均造价为
),中间每个桥墩的平均造价为 万元,桥面每1米长的平均造价为
万元,桥面每1米长的平均造价为 万元.
万元.
(1)试将桥的总造价表示为 的函数
的函数 ;
;
(2)为使桥的总造价最低,试问这座大桥中间(两端桥墩 、
、 除外)应建多少个桥墩?
除外)应建多少个桥墩?
(本小题满分12分)
已知 是等差数列,其中
是等差数列,其中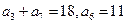 .
.
(Ⅰ)求数列 通项
通项 ;
;
(Ⅱ)若数列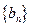 满足
满足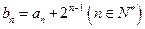 ,求数列
,求数列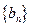 的前
的前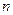 项和
项和 .
.
(本小题满分14分)
设 是椭圆
是椭圆 上的两点,点
上的两点,点 是线段
是线段 的中点,线段
的中点,线段 的垂直平分线与椭圆交于
的垂直平分线与椭圆交于 两点.
两点.
(Ⅰ)当 时,过点P(0,1)且倾斜角为
时,过点P(0,1)且倾斜角为 的直线与椭圆相交于E、F两点,求
的直线与椭圆相交于E、F两点,求 长;
长;
(Ⅱ)确定 的取值范围,并求直线CD的方程.
的取值范围,并求直线CD的方程.
(本小题满分12分)
已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点 (4,
(4, )到焦点的距离为5.
)到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线 相交于不同的两点A、B,求证:
相交于不同的两点A、B,求证:
 .
.
(本小题满分12分)
在锐角 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,且
,且 ,
,
(Ⅰ)求角 ;
;
( Ⅱ)若边
Ⅱ)若边 ,
,  的面积等于
的面积等于 , 求边长
, 求边长 和
和 .
.
(本小题满分12分)
设数列 为等差数列,前
为等差数列,前 项和为
项和为 ,已知
,已知 ,
, ,
,
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列 的前
的前 项和
项和 .
.