(选修4—4:坐标系与参数方程)
在极坐标系中,曲线 的极坐标方程为
的极坐标方程为 ,以极点
,以极点 为原点,极轴为
为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数),试判断直线
为参数),试判断直线 与曲线
与曲线 的位置关系,并说明理由.
的位置关系,并说明理由.
(本小题满分12分)已知数列 的前
的前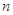 项和为
项和为 ,且
,且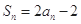 ;数列
;数列 满足
满足 ,
,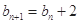 .
.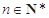 .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)记 ,
,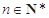 .求数列
.求数列 的前
的前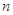 项和
项和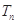 .
.
(本小题满分12分)如图,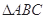 为正三角形,
为正三角形,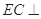 平面
平面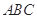 ,
,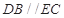 ,
,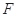 为
为 的中点,
的中点,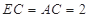 ,
,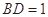 .
.
(Ⅰ)求证:
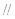 平面
平面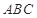 ;
;
(Ⅱ)求多面体 的体积..
的体积..
(本小题满分12分)口袋中装有除编号外其余完全相同的5个小球,编号依次为1,2,3,4,5.现从中同时取出两个球,分别记录下其编号为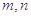 .
.
(Ⅰ)求“ ”的概率;
”的概率;
(Ⅱ)求“ ”的概率.
”的概率.
(本小题满分14分)已知函数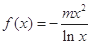 ,
, ,其中
,其中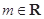 且
且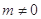 .
. 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当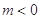 时,求函数
时,求函数 的单调区间和极小值;
的单调区间和极小值;
(Ⅱ)当 时,若函数
时,若函数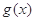 存在
存在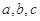 三个零点,且
三个零点,且 ,试证明:
,试证明: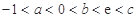 ;
;
(Ⅲ)是否存在负数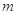 ,对
,对 ,
,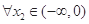 ,都有
,都有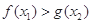 成立?若存在,求出
成立?若存在,求出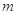 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分13分)已知椭圆 :
: (
(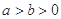 )的右焦点为
)的右焦点为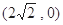 ,且椭圆
,且椭圆 上一点
上一点 到其两焦点
到其两焦点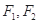 的距离之和为
的距离之和为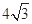 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线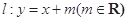 与椭圆
与椭圆 交于不同两点
交于不同两点 ,
, ,且
,且 .若点
.若点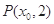 满足
满足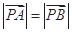 ,求
,求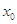 的值.
的值.