【2015高考新课标1,理19】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费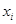 和年销售量
和年销售量 (
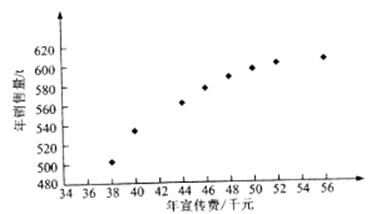
( =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
  |
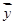 |
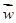 |
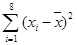 |
 |
 |
 |
| 46.6 |
56.3 |
6.8 |
289.8 |
1.6 |
1469 |
108.8 |
表中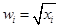 ,
,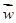 =
=
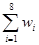
(Ⅰ)根据散点图判断,y=a+bx与y=c+d 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据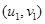 ,
,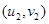 ,……,
,……, ,其回归线
,其回归线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
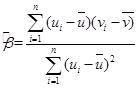 ,
,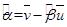
在锐角三角形 中,角
中,角 的对边为
的对边为 ,已知
,已知 ,
, ,
,
(1)求 ;
;
(2)若 ,求
,求 .
.
如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形.除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为 ,其中
,其中 (
( ),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为
),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为 .
.
(1)当k=4时,若要求 为2的倍数,则有多少种不同的标注方法?
为2的倍数,则有多少种不同的标注方法?
(2)当k=11时,若要求 为3的倍数,则有多少种不同的标注方法?
为3的倍数,则有多少种不同的标注方法?
一位网民在网上光顾某网店,经过一番浏览后,对该店铺中的 三种商品有购买意向.已知该网民购买
三种商品有购买意向.已知该网民购买 种商品的概率为
种商品的概率为 ,购买
,购买 种商品的概率为
种商品的概率为 ,购买
,购买 种商品的概率为
种商品的概率为 .假设该网民是否购买这三种商品相互独立.
.假设该网民是否购买这三种商品相互独立.
(1)求该网民至少购买2种商品的概率;
(2)用随机变量 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求 的概率分布和数学期望.
的概率分布和数学期望.
设函数f(x)= +|x-a|(a>0).
+|x-a|(a>0).
(1)证明:f(x)≥2;
(2)若f(3)<5,求实数a的取值范围.
在直角坐标系xOy中,已知曲线 的参数方程是
的参数方程是
 ,在以坐标原点O为极点,
,在以坐标原点O为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 的极坐标方程是
的极坐标方程是 ,求曲线
,求曲线 与
与 的交点在直角坐标系中的直角坐标.
的交点在直角坐标系中的直角坐标.