(本题8分)如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
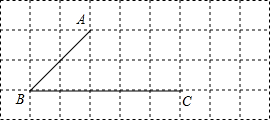
(1)过点C画线段AB的平行线;
(2)过点A画线段BC的垂线,垂足为G,过点A再画线段AB的垂线,交BC于点H;
(3)线段 的长度是点A到直线BC的距离,线段AH的长度是点 到直线 的距离.
(4)线段AG、AH的大小关系为AG<AH,理由是 .
某班同学分三组进行数学活动.对七年级400名同学最喜欢的课余生活情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得的: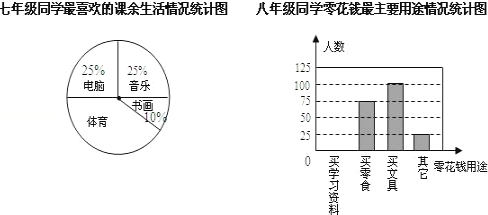
九年级同学完成家庭作业情况统计表
| 时间 |
1小时左右 |
1.5小时左右 |
2小时左右 |
2.5小时左右 |
| 人数 |
50 |
80 |
120 |
50 |
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢“体育”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时?(结果保留一位小数)
已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.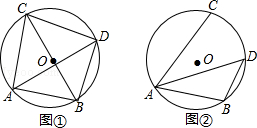
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D。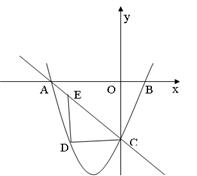
(1)求抛物线的解析式;
(2)当点E的坐标(-2,-1),连接AD,点P在x轴上,使∆APC与∆ADC全等,求出点P的坐标;
(3)当点E在直线AC上运动时,是否存在以D、E、O、C为顶点,OC为一边的平行四边形?若存在,试求出动点E的坐标;若不存在,请说明理由
某商场计划购进冰箱、彩电进行销售,相关信息如下表: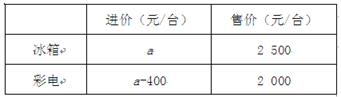
(1)若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等,求表中a的值.
(2)在(1)的条件下,为了满足市场需求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的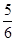 .
.
①该商场有哪几种进货方式?
②若该商场将购进的冰箱、彩电全部售出,获得的最大利润为w元,请用所学的函数知识求出w的值.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.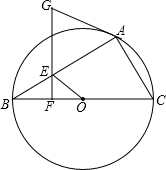
(1)求证:AG与⊙O相切;
(2)若AC=6,AB=8,BE=3,求线段OE的长.