(本小题满分10分)以下是搜集到的开封市祥符区新房屋的销售价格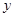 (万元)和房屋的面积
(万元)和房屋的面积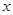 (
(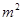 )的数据: 已知变量
)的数据: 已知变量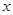 和
和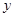 线性相关。
线性相关。
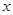 |
80 |
95 |
100 |
110 |
115 |
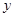 |
18.4 |
21.6 |
23.2 |
24.8 |
27 |
(Ⅰ)求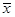 、
、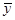 ,及线性回归方程;
,及线性回归方程;
(Ⅱ)据(Ⅰ)的结果估计当房屋面积为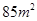 时的销售价格。
时的销售价格。
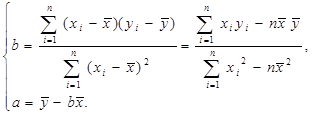
根据统计,组装第x件某产品( ),甲工人所用的时间为
),甲工人所用的时间为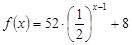 ,乙工人所用的时间为
,乙工人所用的时间为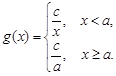 (
(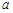 ,
,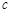 为常数)(单位:分钟).已知乙工人组装第4件产品用时15分钟,组装第
为常数)(单位:分钟).已知乙工人组装第4件产品用时15分钟,组装第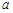 件产品用时10分钟.
件产品用时10分钟.
(Ⅰ)求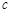 和
和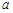 的值;
的值;
(Ⅱ)组装第x件某产品,甲工人的用时是否可能多于乙工人的用时?若可能,求出所有x的值;若不可能,请说明理由.
将一枚质地均匀的骰子连掷两次,记向上的点数分别为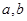 .
.
(Ⅰ)求事件“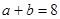 ”的概率;
”的概率;
(Ⅱ)求事件“方程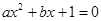 有实根”的概率.
有实根”的概率.
为了估计某校的某次数学期末考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在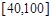 上.将这些成绩分成六段
上.将这些成绩分成六段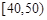 ,
,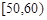 ,…,
,…, 后得到如下部分频率分布直方图.
后得到如下部分频率分布直方图.
(Ⅰ)求抽出的60名学生中分数在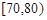 内的人数;
内的人数;
(Ⅱ)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校的优秀人数.
.(本小题共13分)函数 的定义域为R,数列
的定义域为R,数列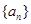 满足
满足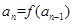 (
( 且
且 ).
).
(Ⅰ)若数列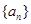 是等差数列,
是等差数列,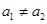 ,且
,且 (k为非零常数,
(k为非零常数,  且
且 ),求k的值;
),求k的值;
(Ⅱ)若 ,
,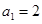 ,
, ,数列
,数列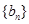 的前n项和为
的前n项和为 ,对于给定的正整数
,对于给定的正整数 ,如果
,如果 的值与n无关,求k的值.
的值与n无关,求k的值.
(本小题共14分)已知函数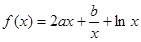 .
.
(Ⅰ)若函数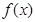 在
在 ,
, 处取得极值,求
处取得极值,求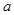 ,
, 的值;
的值;
(Ⅱ)若 ,函数
,函数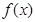 在
在 上是单调函数,求
上是单调函数,求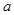 的取值范围.
的取值范围.