为了解高二某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
下面的临界值表供参考:

(参考公式K2=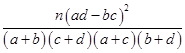 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
设命题p:函数 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式 对一切
对一切 均成立。
均成立。
(Ⅰ)如果p是真命题,求实数 的取值范围;
的取值范围;
(Ⅱ)如果命题“p或q”为真命题,且“p且q”为假命题,求实数 的取值范围.
的取值范围.
已知中心在原点,焦点在坐标轴上的椭圆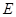 的方程为
的方程为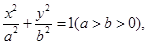 它的离心率为
它的离心率为 ,一个焦点是
,一个焦点是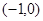 ,过直线
,过直线 上一点引椭圆
上一点引椭圆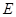 的两条切线,切点分别是A、B.
的两条切线,切点分别是A、B.
(Ⅰ)求椭圆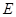 的方程;
的方程;
(Ⅱ)若在椭圆
 上的点
上的点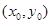 处的切线方程是
处的切线方程是 .求证:直线AB恒过定点,并求出定点的坐标;
.求证:直线AB恒过定点,并求出定点的坐标;
(Ⅲ)记点C为(Ⅱ)中直线AB恒过的定点,问否存在实数 ,使得
,使得 成立,若成立求出
成立,若成立求出 的值,若不存在,请说明理由
的值,若不存在,请说明理由
已知函数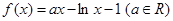 .
.
(Ⅰ)讨论函数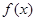 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数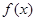 在
在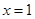 处取得极值,对任意的
处取得极值,对任意的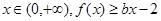 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
在边长为 的菱形
的菱形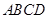 中,
中, .现沿对角线
.现沿对角线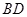 把△
把△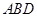 折起,折起后使
折起,折起后使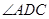 的余弦值为
的余弦值为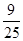 .
.
(Ⅰ)求证:平面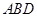 ⊥平面
⊥平面 ;
;
(Ⅱ)若 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.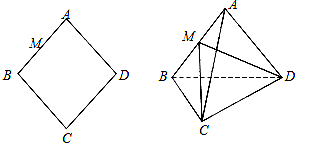
如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?