已知直线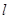 经过点
经过点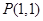 ,倾斜角
,倾斜角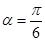 ,
,
(1)写出直线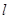 的参数方程。
的参数方程。
(2)设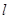 与圆
与圆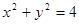 相交于
相交于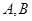 两点,求点
两点,求点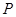 到
到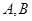 两点的距离之积。
两点的距离之积。
通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
| 男 |
女 |
总计 |
|
| 走天桥 |
40 |
20 |
|
| 走斑马线 |
20 |
30 |
|
| 总计 |
(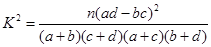 )
)
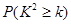 |
0.050 0.010 0.001 |
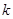 |
3.841 6.635 10.828 |
(1)完成表格
(2)能否在犯错误的概率不超过0.010的前提下认为性别与愿意走斑马线还是愿意走人行天桥有关系。
某种产品的广告费支出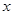 (单位:万元)与销售额
(单位:万元)与销售额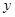 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
广告费支出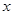 |
2 |
4 |
5 |
6 |
8 |
销售额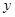 |
30 |
40 |
60 |
50 |
70 |
(1)计算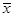 ,
,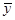 的值并求点
的值并求点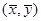 对应的复数
对应的复数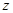 ;
;
(2)完成下表并求回归直线方程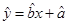 。
。
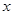 |
2 |
4 |
5 |
6 |
8 |
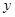 |
30 |
40 |
60 |
50 |
70 |
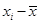 |
|||||
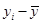 |
|||||
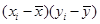 |
|||||
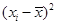 |
( 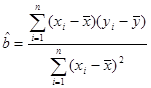 )
)
已知函数f(x)=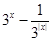 .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若 恒成立,求m的取值范围。
恒成立,求m的取值范围。
已知圆C:x2-4x+y2+2y-3=0内有一点P(1,1),AB为过点P且倾斜角为 的弦。
的弦。
(1)当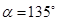 时,求AB的长度;
时,求AB的长度;
(2)求弦AB的最小值,并写出此时的直线方程。