(本小题满分13分)某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
 |
0.010 |
0.005 |
0.001 |
 |
6.635 |
7.879 |
10.828 |
附:
如图,设抛物线方程为 , 为直线 上任意一点,过 引抛物线的切线,切点分别为 .

(Ⅰ)求证:
三点的横坐标成等差数列;
(Ⅱ)已知当
点的坐标为
时,
,求此时抛物线的方程;
(Ⅲ)是否存在点
,使得点
关于直线
的对称点
在抛物线
上,其中,点
满足
(
为坐标原点).若存在,求出所有适合题意的点
的坐标;若不存在,请说明理由.
双曲线M的中心在原点,并以椭圆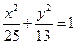 的焦点为焦点,以抛物线
的焦点为焦点,以抛物线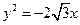 的准线为右准线.
的准线为右准线.
(Ⅰ)求双曲线M的方程;
(Ⅱ)设直线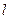 :
: 与双曲线M相交于A、B两点,O是原点.
与双曲线M相交于A、B两点,O是原点.
① 当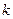 为何值时,使得
为何值时,使得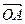
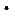

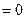 ?
?
② 是否存在这样的实数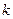 ,使A、B两点关于直线
,使A、B两点关于直线 对称?若存在,求出
对称?若存在,求出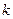 的值;若不存在,说明理由.
的值;若不存在,说明理由.
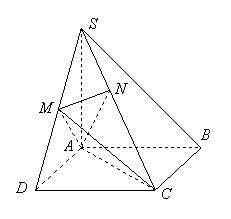
如图,在四棱锥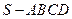 中,底面
中,底面 是正方形,
是正方形,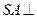 底面
底面 ,
,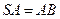 , 点
, 点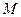 是
是 的中点,
的中点,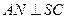 ,且交
,且交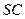 于点
于点 .
.
(I)求证: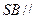 平面
平面 ;
;
(II)求二面角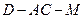 的余弦值大小;
的余弦值大小;
(III)求证:平面 ⊥平面
⊥平面 .
.
已知三次函数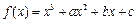 在
在 和
和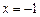 时取极值,且
时取极值,且 .
.
(Ⅰ) 求函数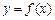 的表达式;
的表达式;
(Ⅱ)求函数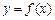 的单调区间和极值;
的单调区间和极值;
(Ⅲ)若函数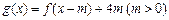 在区间
在区间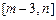 上的值域为
上的值域为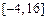 ,试求
,试求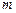 、n应满足的条件。
、n应满足的条件。
设 是平面上的两个向量,且
是平面上的两个向量,且 互相垂直.
互相垂直.
(1)求λ的值;
(2)若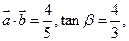 求
求 的值.
的值.