如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE= AC,连接CE、OE,连接AE交OD于点F.
AC,连接CE、OE,连接AE交OD于点F.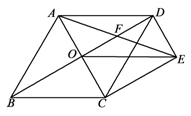
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
(本小题满分14分)已知函数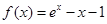 ,
, , 其中,
, 其中,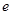 是自然对数的底数.函数
是自然对数的底数.函数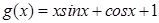 ,
,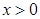 .
.
(Ⅰ)求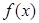 的最小值;
的最小值;
(Ⅱ)将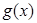 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列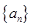 ,求证:
,求证:
(1)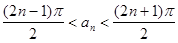 ,其中
,其中 ;
;
(2)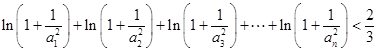 .
.
(本小题满分13分)如图,已知抛物线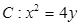 ,过焦点F任作一条直线与
,过焦点F任作一条直线与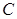 相交于
相交于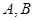 两点,过点
两点,过点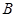 作
作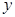 轴的平行线与直线
轴的平行线与直线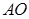 相交于点
相交于点 (
( 为坐标原点).
为坐标原点).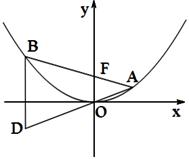
(Ⅰ)证明:动点 在定直线上;
在定直线上;
(Ⅱ)点P为抛物线C上的动点,直线 为抛物线C在P点处的切线,求点Q(0,4)到直线
为抛物线C在P点处的切线,求点Q(0,4)到直线 距离的最小值.
距离的最小值.
(本小题满分13分)在四棱锥 中,
中, ,
,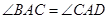
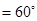 ,
,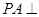 平面
平面 ,直线PC与平面ABCD所成角为
,直线PC与平面ABCD所成角为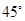 ,
,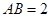 .
.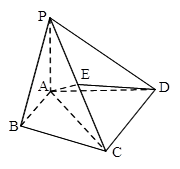
(Ⅰ)求四棱锥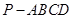 的体积
的体积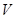 ;
;
(Ⅱ)若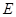 为
为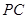 的中点,求证:平面
的中点,求证:平面
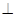 平面
平面 .
.
本小题满分13分)设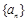 是公比为q的等比数列.
是公比为q的等比数列.
(Ⅰ)推导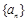 的前n项和公式;
的前n项和公式;
(Ⅱ)设q≠1, 证明数列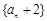 不是等比数列.
不是等比数列.
(本小题满分12分)已知向量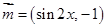 ,向量
,向量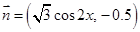 ,函数
,函数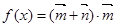 .
.
(Ⅰ)求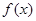 的最小正周期
的最小正周期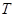 ;
;
(Ⅱ)已知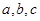 分别为
分别为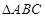 内角
内角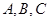 的对边,
的对边,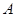 为锐角,
为锐角,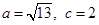 ,且
,且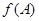 恰是
恰是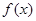 在
在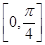 上的最大值,求
上的最大值,求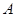 和
和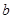 .
.