【问题探究】
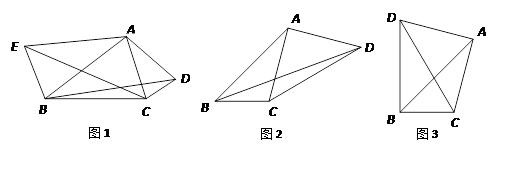
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45º,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
已知数列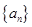 的各项均不为0,其前n项和为
的各项均不为0,其前n项和为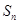 ,且满足
,且满足 ,
,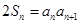 .
.
(1)求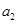 的值;
的值;
(2)求证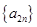 是等差数列;
是等差数列;
(3)若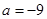 ,求数列
,求数列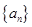 的通项公式
的通项公式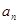 ,并求
,并求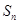
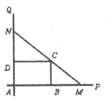
如下图,互相垂直的两条公路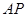 、
、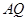 旁有一矩形花园
旁有一矩形花园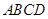 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园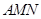 ,要求点
,要求点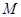 在射线
在射线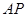 上,点N在射线
上,点N在射线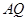 上,且直线
上,且直线 过点
过点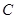 ,其中
,其中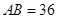 米,
米,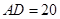 米.记三角形花园
米.记三角形花园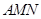 的面积为
的面积为 .
.
(1)问: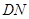 取何值时,
取何值时, 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(2)若 不超过1764平方米,求
不超过1764平方米,求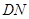 长的取值范围.
长的取值范围.
函数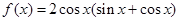 .
.
(1)求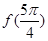 的值;
的值;
(2)求函数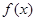 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
设函数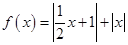 (
( )的最小值为
)的最小值为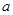 .
.
(1)求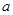 ;
;
(2)已知两个正数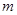 ,
,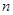 满足
满足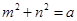 ,求
,求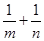 的最小值.
的最小值.
已知在平面直角坐标系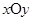 中,直线
中,直线 的参数方程是
的参数方程是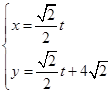 (
( 是参数),以原点
是参数),以原点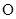 为极点,
为极点,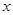 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线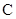 的极坐标方程为
的极坐标方程为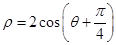 .
.
(1)判断直线 与曲线
与曲线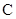 的位置关系;
的位置关系;
(2) 为曲线
为曲线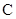 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.