若 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.
(1)求n的值及展开式中二项式系数最大的项.
(2)此展开式中是否有常数项,为什么?
(本小题满分14分)
已知函数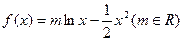
 满足
满足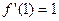 .
.
(1)求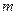 的值及函数
的值及函数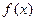 的单调区间;
的单调区间;
(2)若函数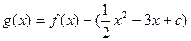 在
在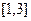 内有两
内有两 个零点,求实数
个零点,求实数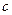 的取值范围.
的取值范围.
(本小题满分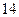 分)
分)
已知椭圆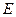 的中心在坐标原点
的中心在坐标原点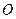 ,两个焦点分别为
,两个焦点分别为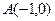 、
、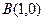 ,一个顶点为
,一个顶点为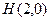 .
.
(1)求椭圆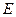 的标准方程;
的标准方程;
(2)对于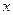 轴上的点
轴上的点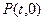 ,椭圆
,椭圆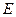 上存在点
上存在点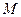 ,使得
,使得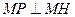 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分)
在三棱锥 中,
中,
 是边长为
是边长为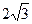 的正三角形,平面
的正三角形,平面 ⊥平面
⊥平面 ,
,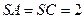 ,
, 、
、 分别为
分别为 、
、 的中点。
的中点。
(1)证明: ⊥
⊥ ;
;
(2)求三棱锥 的体积.
的体积.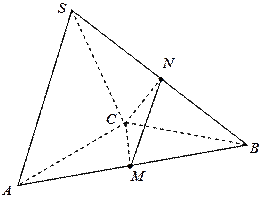
(本小题满分 分)
分)
为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.
规定评估的平均得分与全市的总体交通状况等级如下表:
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;
(2)用简单随机抽样方法从这 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的 绝对值不超过
绝对值不超过 的概率.
的概率.
(本小题满分 分)
分)
已知函数 .
.
(1)求函数 的最大值;
的最大值;
(2)在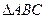 中,
中,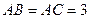 ,角
,角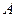 满足
满足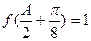 ,求
,求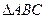 的面积.
的面积.