某商场的销售部经过市场调查发现,该商场的某种商品每日的销售量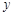 (单位:千克)与销售价格
(单位:千克)与销售价格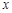 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 ,
,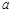 为常数,已知销售价格为
为常数,已知销售价格为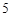 元/千克时,每日可售出该商品
元/千克时,每日可售出该商品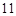 千克.
千克.
(Ⅰ)求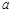 的值;
的值;
(Ⅱ)若该商品的成本为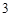 元/千克,试确定销售价格
元/千克,试确定销售价格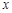 的值,使该商场每日销售该商品所获得的利润最大.
的值,使该商场每日销售该商品所获得的利润最大.
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子任取2个球,乙从箱子里在取1个球,若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的数学期望.
已知10件不同的产品中共有3件次品,现对它们进行一一测试,直到找出所有3件次品为止.
(1)求恰好在第5次测试时3件次品全部被测出的概率;
(2)记恰好在第k次测试时3件次品全部被测出的概率为f(k),求f(k)的最大值和最小值.
甲与乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n.
(1)算国徽面朝上不同次数的概率并填入下表:
(2)现规定:若m>n,则甲胜;若n≥m,则乙胜.你认为这种规定合理吗?为什么?
某校高三一次月考之后,为了了解数学学科的学习情况,现从中随机抽出若干名学生此次的数学成绩,按成绩分组,制成下面频率分布表:
(1)若每组数据用该区间的中点值(例如区间[90,100 )的中点值是95)作为代表,试估计该校高三学生本次月考的平均分;
(2)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩,并记成绩落在区间[110,130 )中的学生数为ξ,求:
①在三次抽取过程中至少两次连续抽中成绩在区间[110,130 )中的概率;
②ξ的分布列和数学期望.
在袋子中装有10个大小相同的小球,其中黑球有3个,白球有n(2≤n≤5,且n≠3)个,其余的球为红球.
(Ⅰ)若n=5,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
(Ⅱ)从袋里任意取出2个球,如果这两个球的颜色相同的概率是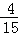 ,求红球的个数;
,求红球的个数;
(Ⅲ)在(Ⅱ)的条件下,从袋里任意取出2个球.若取出1个白球记1分,取出1个黑球记2分,取出1个红球记3分.用ξ表示取出的2个球所得分数的和,写出ξ的分布列,并求ξ的数学期望Eξ.