对定义域分别为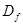 、
、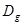 的函数
的函数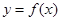 、
、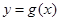 ,规定:
,规定:
函数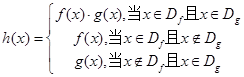 .
.
(1)若函数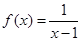 ,
,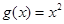 ,写出函数
,写出函数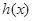 的解析式;
的解析式;
(2)求问题(1)中函数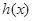 的值域.
的值域.
设A、B是两个非空集合,定义A与B的差集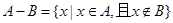 .
.
(1)试举出两个数集,使它们的差集为单元素集合;
(2)差集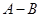 与
与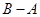 是否一定相等?请说明理由;
是否一定相等?请说明理由;
(3)已知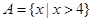 ,
,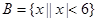 ,求
,求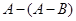 及
及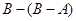 ,由此你可以得到什么更一般的结论?(不必证明)
,由此你可以得到什么更一般的结论?(不必证明)
求下列函数的值域.
(1)求函数 的值域.
的值域.
(2) 求函数 的值域.
的值域.
(3)求函数 ,
, 的值域.
的值域.
(本小题满分10分) 选修4—5:不等式选讲.
已知函数 .
.
(1)若不等式 恒成立,求
恒成立,求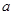 的取值范围;
的取值范围;
(2)当 时,求:不等式
时,求:不等式 的解集.
的解集.
(本小题满分10分) 选修4—4:坐标系与参数方程.
已知曲线 的参数方程为
的参数方程为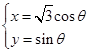 (
(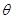 为参数),直线
为参数),直线 的极坐标方程为
的极坐标方程为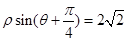 .
.
(1)写出曲线 的普通方程和直线
的普通方程和直线 的直角坐标方程;
的直角坐标方程;
(2)设点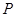 为曲线
为曲线 上的动点,求点
上的动点,求点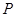 到直线
到直线 距离的最大值.
距离的最大值.