已知全集U=R,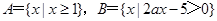 ,
,
(1)若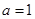 ,求
,求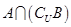 .
.
(2)若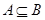 ,求
,求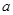 的取值范围。
的取值范围。
已知圆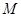 :
: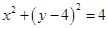 ,点
,点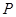 是直线
是直线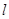 :
: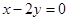 上的一动点,过点
上的一动点,过点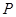 作圆M的切线
作圆M的切线 、
、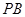 ,切点为
,切点为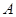 、
、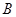 .
.
(Ⅰ)当切线PA的长度为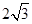 时,求点
时,求点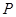 的坐标;
的坐标;
(Ⅱ)若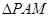 的外接圆为圆
的外接圆为圆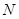 ,试问:当
,试问:当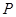 运动时,圆
运动时,圆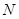 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
(Ⅲ)求线段 长度的最小值.
长度的最小值.
如图所示,已知ABCD为梯形, ,且
,且 ,
, 为线段PC上一点.
为线段PC上一点.
(1)当 时,证明:
时,证明: ;
;
(2)设平面 ,证明:
,证明:
(3)在棱PC上是否存在点 ,使得
,使得 ,若存在,请确定点
,若存在,请确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
如图,在四棱锥 中,底面
中,底面 是正方形,侧面
是正方形,侧面
 底面
底面 ,且
,且 ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
(Ⅰ)求证:直线 ∥平面
∥平面 ;
;
(Ⅱ)求证:直线
 平面
平面 .
.