(本小题满分12分)已知函数 的图象如图,直线
的图象如图,直线 在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为
在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为 .
.
(1)求 的解析式;
的解析式;
(2)若常数 ,求函数
,求函数 在区间
在区间 上的最大值.
上的最大值.
已知椭圆 ,
, 分别为左顶点和上顶点,F为右焦点,过F作
分别为左顶点和上顶点,F为右焦点,过F作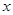 轴的垂线交椭圆于点C,且直线
轴的垂线交椭圆于点C,且直线 与直线OC平行.
与直线OC平行.
(1)求椭圆的离心率;
(2)已知定点M( ),
),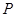 为椭圆上的动点,若
为椭圆上的动点,若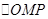 的重心轨迹经过点
的重心轨迹经过点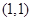 ,求椭圆的方程.
,求椭圆的方程.
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击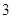 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率;
(3)如果在靶上画一个边长为 的等边
的等边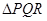 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形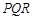 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形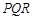 内。求弹孔与
内。求弹孔与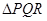 三个顶点的距离都大于1的概率(忽略弹孔大小).
三个顶点的距离都大于1的概率(忽略弹孔大小).
已知命题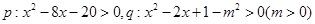 ,若
,若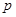 是
是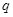 的充分不必要条件,求实数
的充分不必要条件,求实数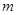 的取值范围.
的取值范围.
已知椭圆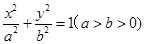 的离心率
的离心率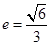 ,过点
,过点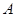
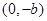 和
和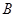
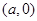 的直线与原点的距离为
的直线与原点的距离为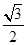 .
.
(1)求椭圆的方程;
(2)设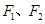 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过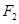 作直线交椭圆于
作直线交椭圆于 、
、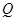 两点,求
两点,求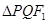 的内切圆半径
的内切圆半径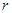 的最大值
的最大值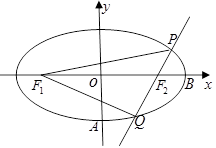
已知函数f(x)=ax3+bx2-3x在x=±1处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4;
(Ⅲ)若过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求实数m的取值范围.