为了治理大气污染,我国中部某市抽取了该市2014年中120天的空气质量指数,绘制了如下不完整的统计图表:
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a= ,m= ;
(2)请把空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是 度;
(4)估计该市2014年(365天)中空气质量指数大于100的天数约有 天.
如图,抛物线 经过点 ,点 ,作 轴交抛物线于点 ,作 轴,垂足为 ,动点 从点 出发在线段 上以每秒2个单位长度的速度向点 运动,同时动点 从点 出发在线段 上以每秒1个单位长度的速度向点 运动,当一个点到达终点时,另一个点也随之停止运动,设运动时间为 秒.
(1)求抛物线的解析式;
(2)设 的面积为 ,求 与 的函数关系式;
(3)①当 时,直接写出 的值;
②在点 和点 运动过程中,是否存在某一时刻,使 ?若存在,直接写出此时 的值;若不存在,请说明理由.

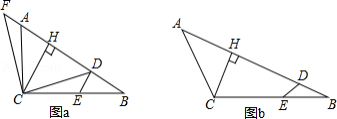
如图,在 中, ,点 在 上, ,点 在 上,连接 , ,作 ,垂足为 .
(1)如图 ,当 时,连接 ,过点 作 交 的延长线于点 .
①求证: ;
②请猜想三条线段 , , 之间的数量关系,直接写出结论;
(2)如图 ,当 时,三条线段 , , 之间存在怎样的数量关系?请证明你的结论.
有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润 (万元)与投资成本 (万元)满足如图①所示的二次函数 ;种植柏树的利润 (万元)与投资成本 (万元)满足如图②所示的正比例函数 .
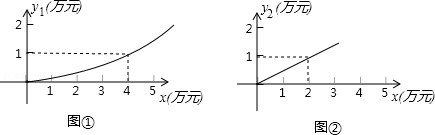
(1)分别求出利润 (万元)和利润 (万元)关于投资成本 (万元)的函数关系式;
(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
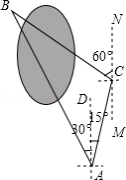
小明要测量公园被湖水隔开的两棵大树 和 之间的距离,他在 处测得大树 在 的北偏西 方向,他从 处出发向北偏东 方向走了200米到达 处,测得大树 在 的北偏西 方向.
(1)求 的度数;
(2)求两棵大树 和 之间的距离(结果精确到1米)(参考数据: , ,
如图, 是 的直径,点 是 上一点,连接 , ,作 ,垂足为 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积.
