某同学参加语、数、外三门课程的考试,设该同学语、数、外取得优秀成绩的概率分别为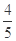 ,m,n(m>n),设该同学三门课程都取得优秀成绩的概率为
,m,n(m>n),设该同学三门课程都取得优秀成绩的概率为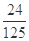 ,都未取得优秀成绩的概率为
,都未取得优秀成绩的概率为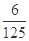 ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.
(1)求m,n;
(2)设X为该同学取得优秀成绩的课程门数,求EX.
(本题满分14分)
已知点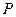 是⊙
是⊙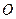 :
: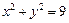 上的任意一点,过
上的任意一点,过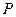 作
作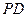 垂直
垂直 轴于
轴于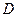 ,动点
,动点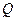 满足
满足 。
。
(1)求动点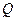 的轨迹方程;
的轨迹方程;
(2)已知点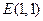 ,在动点
,在动点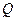 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点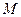 、
、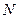 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线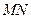 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
(本题满分13分)
如图,在六面体 中,平面
中,平面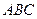 ∥平面
∥平面 ,
,
⊥平面 ,
, ,
, ,
,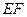 ∥
∥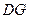 .且
.且 ,
, .
.
(1)求证: 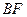 ∥平面
∥平面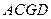 ;
;
(2)求二面角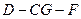 的余弦值;
的余弦值;
(3) 求五面体 的体积.
的体积.
(本题满分13分)
已知三次函数 的导函数
的导函数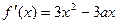 ,
,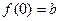 ,
, 、
、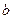 为实数。
为实数。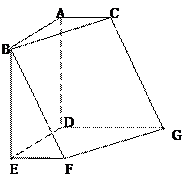
(1)若曲线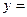
 在点(
在点( ,
,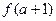 )处切线的斜率为12,求
)处切线的斜率为12,求 的值;
的值;
(2)若 在区间[-1,1]上的最小值、最大值分别为-2、1,且
在区间[-1,1]上的最小值、最大值分别为-2、1,且 ,求函数
,求函数 的解析式。
的解析式。
(本题满分13分)
某学校数学兴趣小组有10名学生,其中有4名女同学;英语兴趣小组有5名学生,其中有3名女学生,现采用分层抽样方法(层内采用不放回简单随机抽样)从数学兴趣小组、英语兴趣小组中共抽取3名学生参加科技节活动。
(1)求从数学兴趣小组、英语兴趣小组各抽取的人数;
(2)求从数学兴趣小组抽取的学生中恰有1名女学生的概率;
(3)记 表示抽取的3名学生中男学生数,求
表示抽取的3名学生中男学生数,求 的分布列及数学期望。
的分布列及数学期望。
已知数列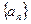 中,
中,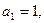 且点
且点 在直线
在直线 上.
上.
(1)求数列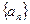 的通项公式;
的通项公式;
(2)若函数
求函数 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前
的前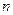 项和.试问:是否存在关于
项和.试问:是否存在关于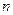 的整式
的整式 ,使得
,使得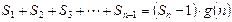 对于一切不小于2的自然数
对于一切不小于2的自然数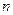 恒成立? 若存在,写出
恒成立? 若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。