如图，在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M、N，直线m运动的时间为t（秒）．
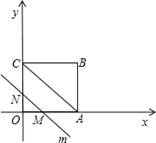
（1）点A的坐标是 ，点C的坐标是 ；
（2）当t= 秒或 秒时，MN=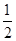
AC；
（3）设△OMN的面积为S，求S与t的函数关系式．
（年贵州省黔东南州）去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．
（1）求饮用水和蔬菜各有多少件？
（2）现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；
（3）在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？
（年云南省昆明市）某部队将在指定山区进行军事演习，为了使道路便于部队重型车辆通过，部队工兵连接到抢修一段长3600米道路的任务，按原计划完成总任务的
后，为了让道路尽快投入使用，工兵连将工作效率提高了50%，一共用了10小时完成任务．
（1）按原计划完成总任务的时，已抢修道路 米；
（2）求原计划每小时抢修道路多少米？
（年贵州省铜仁市）2015年5月，某县突降暴雨，造成山体滑坡，挢梁垮塌，房屋大面积受损，该省民政厅急需将一批帐篷送往灾区．现有甲、乙两种货车，己知甲种货车比乙种货车每辆车多装20件帐篷，且甲种货车装运1000件帐篷所用车辆与乙种货车装运800件帐蓬所用车辆相等．
（1）求甲、乙两种货车每辆车可装多少件帐蓬？
（2）如果这批帐篷有1490件，用甲、乙两种汽车共16辆来装运，甲种车辆刚好装满，乙种车辆最后一辆只装了50件，其它装满，求甲、乙两种汽车各有多少辆？
（年云南省曲靖市）某商场投入13800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：
（1）该商场购进甲、乙两种矿泉水各多少箱？
（2）全部售完500箱矿泉水，该商场共获得利润多少元？
（年贵州省黔东南州）解不等式组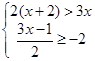
，并将它的解集在数轴上表示出来．