据调查，超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学用所学过的知识在一条笔直的道路上检测车速．如图，观测点C到公路的距离CD为100米，检测路段的起点A位于点C的南偏西60°方向上，终点B位于点C的南偏西45°方向上．某时段，一辆轿车由西向东匀速行驶，测得此车由A处行驶到B处的时间为4秒．问此车是否超过了该路段16米/秒的限制速度？（参考数据：
≈1．4，
≈1．7）
已知：如图，点D是△ABC内一点，AB=AC，∠1=∠2．求证：AD平分∠BAC．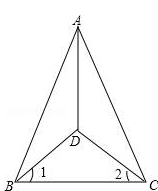
上个月，商店共卖出甲、乙两种商品1000件，这个月甲商品多卖出50%，乙商品少卖出10%，结果产品的总销量减少了4%，上个月甲、乙两种商品各卖出多少件？
解下列各题：
（1）解方程组
（2）化简：
（3）解不等式：
≤
，并把它的解集表示在数轴上
（4）解不等式组：
，并把它的解集表示在数轴上．
已知抛物线y=ax2+bx+3与y轴的交点为A，点A与点B关于抛物线的对称轴对称，二次函数y=ax2+bx+3的y与x的部分对应值如下表：
| x |
… |
﹣1 |
0 |
1 |
3 |
4 |
… |
| y |
… |
8 |
0 |
0 |
… |
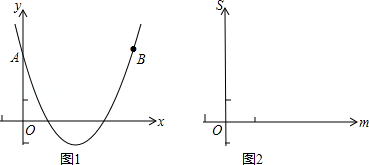
（1）抛物线的对称轴是_________ ．点A（______，____），B（_____，_____）；
（2）求二次函数y=ax2+bx+3的解析式；
（3）已知点M（m，n）在抛物线y=ax2+bx+3上，设△BAM的面积为S，求S与m的函数关系式、画出函数图象．并利用函数图象说明S是否存在最大值，为什么？
某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）与每件销售价x（元）的关系数据如下：
| x |
30 |
32 |
34 |
36 |
| y |
40 |
36 |
32 |
28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式；（不写出自变量x的取值范围）
（2）如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？