在矩形中
中，
，
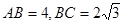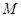为动点，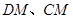
的延长线与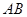
（或其延长线）分别交于点
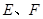，若
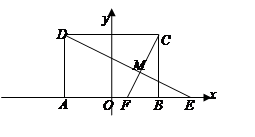
（1）若以线段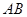所在的直线为
轴，线段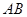的中垂线为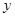
轴建立平面直角坐标系，试求动点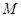的轨迹方程；
（2）不过原点的直线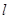
与（1）中轨迹交于
两点，若
的中点
在抛物线
上，求直线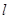的斜率
的取值范围．
已知指数函数
满足：
，定义域为
的函数
是奇函数．
（1）确定
和的解析式；
（2）判断函数
的单调性，并用定义证明；
（3）若对于任意
，都有
成立，求
的取值范围．
某种商品在
天内每件的销售价格
（元）与时间
（天）的函数关系用如图表示，该商品在天内日销售量
（件）与时间（天）之间的关系如下表：
（1）根据提供的图象（如图），写出该商品每件的销售价格与时间的函数关系式；
（2）根据表
提供的数据，写出日销售量与时间的一次函数关系式；
（3）求该商品的日销售金额的最大值，并指出日销售金额最大的一天是天中的第几天．（日销售金额
每件的销售价格
日销售量）
设
．
（1）若
，判断并证明函数
的奇偶性；
（2）令
，
，当
取何值时
取得最小值，最小值为多少？
若
是定义在
上的增函数，且对一切
，
，满足
．
（1）求
的值；
（2）若
，解不等式
．
求值：
（1）
；
（2）