某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
| 岗位 |
经理 |
技师 |
领班 |
助理 |
服务员 |
清洁工 |
| 基本工资 |
10000 |
4000 |
2400 |
1600 |
|
1000 |
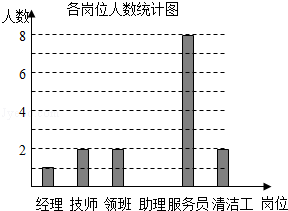
请回答下列问题:
(1)将各岗位人数统计图补充完整;
(2)求该公司服务员每人的基本工资;
(3)该公司所有员工基本工资的中位数是 元,众数是 元;你认为用基本工资的平均数和中位数来代表该公司员工基本工资的一般水平,哪一个更恰当?请说明理由.
(4)该公司一名员工向经理辞职了,若其他员工的基本工资不变,那么基本工资的平均数就降低了.你认为辞职的可能是哪个岗位上的员工呢?说明理由.
关于x的一元二次方程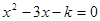 有两个不相等的实数根.
有两个不相等的实数根.
(1)求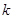 的取值范围;
的取值范围;
(2)若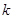 为符合条件的最小整数,求此时方程的根.
为符合条件的最小整数,求此时方程的根.
已知:二次函数的图象经过原点,对称轴是直线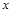 =-2,最高点的纵坐标为4,求:该二次函数解析式。
=-2,最高点的纵坐标为4,求:该二次函数解析式。
如图抛物线过坐标原点O和x轴上另一点E,顶点M为 (2,4);矩形ABCD顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速从图示位置沿x轴正方向匀速平行移动,同时一动点P也以相同速度从点A出发向B匀速移动,设它们运动时间为t秒(0≤t≤3),直线AB与该抛物线交点为N
① 当t= 时,判断点P是否在直线ME上,说明理由;
时,判断点P是否在直线ME上,说明理由;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?说明理由.
如图1,在正方形 中,对角线
中,对角线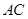 与
与 相交于点
相交于点 ,
, 平分
平分 ,交
,交 于点
于点 .
.
(1)求证: ;
;
(2)点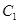 从点
从点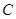 出发,沿着线段
出发,沿着线段 向点
向点 运动(不与点
运动(不与点 重合),同时点
重合),同时点 从点
从点 出发,沿着
出发,沿着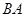 的延长线运动,点
的延长线运动,点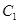 与
与 的运动速度相同,当动点
的运动速度相同,当动点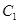 停止运动时,另一动点
停止运动时,另一动点 也随之停止运动.如图2,
也随之停止运动.如图2, 平分
平分 ,交
,交 于点
于点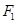 ,过点
,过点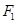 作
作 ,垂足为
,垂足为 ,请猜想
,请猜想 ,
, 与
与 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当 ,
,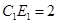 时,求
时,求 的长
的长
(本小题满分9分)
如图一次函数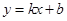 (
( )的图象分别交
)的图象分别交 轴、
轴、 轴于点
轴于点 ,与反比例函数
,与反比例函数 图象在第二象限交于点
图象在第二象限交于点 ,
,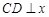 轴于点
轴于点 ,OA=OD.
,OA=OD.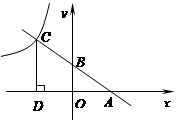
⑴求m的值和一次函数的表达式;
⑵在 轴上求点
轴上求点 ,使△CAP为等腰三角形(求出所有符合条件的点).
,使△CAP为等腰三角形(求出所有符合条件的点).