(本小题满分14分)已知椭圆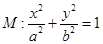
 的离心率为
的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为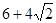 .
.
(Ⅰ)求椭圆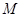 的方程;
的方程;
(Ⅱ)设直线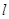 与椭圆
与椭圆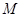 交于
交于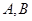 两点,且以
两点,且以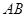 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点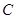 ,
,
求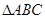 面积的最大值.
面积的最大值.
(本小题满分12分)
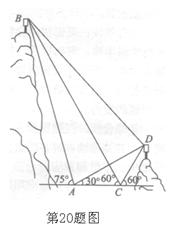
如图, 都在同一个与水平面垂直的平面内,
都在同一个与水平面垂直的平面内, 为两岛上的两座灯塔的塔顶. 测量船于水面
为两岛上的两座灯塔的塔顶. 测量船于水面 处测得
处测得 点和
点和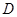 点的仰角分别为
点的仰角分别为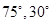 ,于水面
,于水面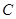 处测得
处测得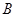 点和
点和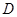 点的仰角均为
点的仰角均为 ,
, .试探究图中
.试探究图中 间距离与另外哪两点间距离相等,然后求
间距离与另外哪两点间距离相等,然后求 间的距离。(计算结果精确到
间的距离。(计算结果精确到 )
)
参考数据: ,
,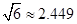
(本小题满分12分);
已知过抛物线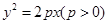 的焦点,斜率为
的焦点,斜率为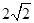 的直线交抛物线于不同两点
的直线交抛物线于不同两点 ,且
,且 .
.
(1)求该抛物线的方程;
(2) 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若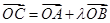 ,求
,求 的值。
的值。
(本小题满分12分)
在数列 中,
中, .
.
(1)设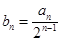 ,证明:数列
,证明:数列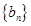 是等差数列;
是等差数列;
(2)求数列 的前
的前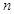 项和
项和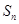 .
.
(本小题满分12分)
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量(万吨) |
236 |
246 |
257 |
276 |
286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程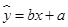 ;
;
(2)利用(1)中所求出的直线方程预测该地2012年的粮食需求量.(温馨提示:答题前请仔细阅读卷首所给出的计算公式)
已知数列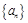 的首项
的首项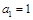 ,前n项之和
,前n项之和 满足关系式:
满足关系式: .
.
(1)求证:数列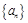 是等比数列;
是等比数列;
(2)设数列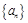 的公比为
的公比为 ,数列
,数列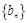 满足
满足 ,且
,且 .
.
(i)求数列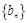 的通项
的通项 ;
;
(ii)设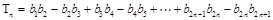 ,求
,求 .
.