阅读材料：如图1，△ABC的周长为l，面积为S，内切圆O的半径为r，探究r与S、l之间的关系．
连接OA，OB，OC
∵S=S△OAB+S△OBC+S△OCA
又∵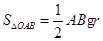
，
，
∴
∴
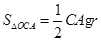
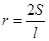
解决问题：
（1）利用探究的结论，计算边长分别为5，12，13的三角形内切圆半径；
（2）若四边形ABCD存在内切圆（与各边都相切的圆），如图2且面积为S，各边长分别为a，b，c，d，试推导四边形的内切圆半径公式；
（3）若一个n边形（n为不小于3的整数）存在内切圆，且面积为S，各边长分别为a1，a2，a3，…，an，合理猜想其内切圆半径公式（不需说明理由）．
（年湖南常德10分）如图，已知二次函数的图象过点O（0，0），A（4，0），B（2，
），M是OA的中点．
（1）求此二次函数的解析式；
（2）设P是抛物线上的一点，过P作x轴的平行线与抛物线交于另一点Q，要使四边形PQAM是菱形，求P点的坐标；
（3）将抛物线在x轴下方的部分沿x轴向上翻折，得曲线OB′A（B′为B关于x轴的对称点），在原抛物线x轴的上方部分取一点C，连接CM，CM与翻折后的曲线OB′A交于点D．若△CDA的面积是△MDA面积的2倍，这样的点C是否存在？若存在求出C点的坐标，若不存在，请说明理由．
（年湖北黄冈13分）如图，在四边形OABC中，AB∥OC，BC⊥x轴于C，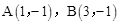
，动点P从O点出发，沿x轴正方向以2个单位/秒的速度运动．过P作PQ⊥OA于Q．设P点运动的时间为t秒（0 < t < 2），ΔOPQ与四边形OABC重叠的面积为S．
（1）求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标；
（2）用含t的代数式表示P、Q两点的坐标；
（3）将ΔOPQ绕P点逆时针旋转90°，是否存在t，使得ΔOPQ的顶点O或Q落在抛物线上？若存在，直接写出t的值；若不存在，请说明理由；
（4）求S与t的函数解析式.
（年黑龙江牡丹江农垦10分）如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．
（1）求线段CD的长；
（2）设△CPQ的面积为S，求S与t之间的函数关系式，并确定在运动过程中是否存在某一时刻t，使得S△CPQ：S△ABC=9：100？若存在，求出t的值；若不存在，说明理由．
（3）当t为何值时，△CPQ为等腰三角形？
（年贵州六盘水16分）如图，二次函数
的图象交x轴于A、D两点，并经过B点，已知A点坐标是（2，0），B点的坐标是（8，6）．
（1）求二次函数的解析式．
（2）求函数图象的顶点坐标及D点的坐标．
（3）该二次函数的对称轴交x轴于C点．连接BC，并延长BC交抛物线于E点，连接BD，DE，求△BDE的面积．
（4）抛物线上有一个动点P，与A，D两点构成△ADP，是否存在S△ADP=
S△BCD？若存在，请求出P点的坐标；若不存在．请说明理由．
（年广西南宁10分）在平面直角坐标系中, 抛物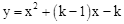线
与直线
交于A, B两点，点A在点B的左侧.
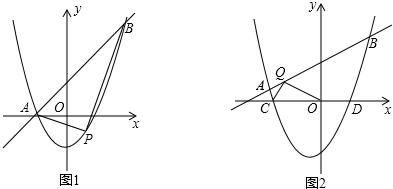
（1）如图1，当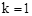
时，直接写出A，B两点的坐标；
（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
（3）如图2，抛物线
与x轴交于C，D两点（点C在点D的左侧）.在直线上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k的值；若不存在，请说明理由.