如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.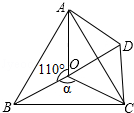
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具售价不能高于40元. 设每件玩具的销售单价上涨了x元时(x为正整数),月销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每件玩具的售价定为多少元时,月销售利润恰为2520元?
(3)每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
用长为20cm的铁丝,折成一个矩形,设它的一边长为xcm,面积为ycm2。
(1)求出y与x的函数关系式
(2)当边长x为多少时,矩形的面积最大,最大面积是多少?
如图,正方形网格中,△ABC 为格点三角形(顶点都是格点),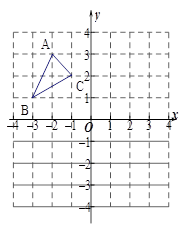
(1)将△ABC绕点O按逆时针方向旋转90°得到△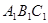
(2)将△ABC绕原点O旋转180°,画出旋转后的△
已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
用适当的方法解下列方程:
(1)
(2)x2-4x+1=0