(本小题满分14分)已知函数 .
.
(1)证明: ;
;
(2)比较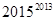 与
与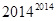 的大小;
的大小;
(3)给定正整数 ,
, 个正实数
个正实数 ,
, ,…,
,…, 满足
满足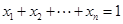 ,证明:
,证明:
离心率为 的椭圆
的椭圆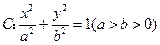 上有一点
上有一点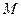 到椭圆两焦点的距离和为
到椭圆两焦点的距离和为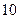 .以椭圆
.以椭圆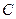 的右焦点
的右焦点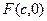 为圆心,短轴长为直径的圆有切线
为圆心,短轴长为直径的圆有切线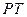 (
(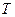 为切点),且点
为切点),且点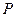 满足
满足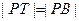 (
(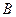 为椭圆
为椭圆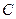 的上顶点)。(I)求椭圆的方程;(II)求点
的上顶点)。(I)求椭圆的方程;(II)求点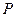 所在的直线方程
所在的直线方程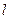 .
.
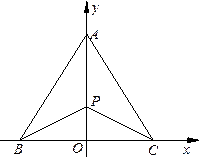 有三个生活小区,分别位于
有三个生活小区,分别位于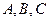 三点处,且
三点处,且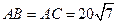 ,
,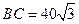 . 今计划合建一个变电站,为同时方便三个小区,准备建在
. 今计划合建一个变电站,为同时方便三个小区,准备建在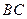 的垂直平分线
的垂直平分线
上的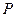 点处,建立坐标系如图,且
点处,建立坐标系如图,且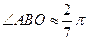 .
.
(Ⅰ)若希望变电站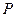 到三个小区的距离和最小,
到三个小区的距离和最小,
点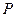 应位于何处?
应位于何处?
(Ⅱ)若希望点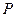 到三个小区的最远距离为最小,
到三个小区的最远距离为最小,
点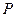 应位于何处?
应位于何处?
已知函数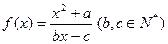 ,若方程
,若方程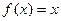 有且只有两个相异根0和2,且
有且只有两个相异根0和2,且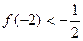
(1)求函数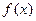 的解析式。
的解析式。
(2)已知各项不为1的数列{an}满足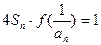 ,求数列通项an。
,求数列通项an。
(3)如果数列{bn}满足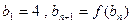 ,求证:当
,求证:当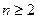 时,恒有
时,恒有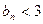 成立。
成立。
已知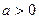 ,函数
,函数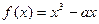 ,在
,在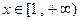 是一个单调函数。
是一个单调函数。
(1)试问 在
在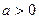 的条件下,在
的条件下,在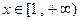 能否是单调递减函数?说明理由。
能否是单调递减函数?说明理由。
(2)若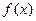 在
在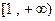 上是单调递增函数,求实数a的取值范围。
上是单调递增函数,求实数a的取值范围。
(3)设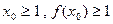 且
且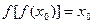 ,比较
,比较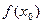 与
与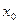 的大小。
的大小。
已知函数 (其中
(其中 )的图象与x轴在原点右侧的第一个交点为N(6,0),又
)的图象与x轴在原点右侧的第一个交点为N(6,0),又
(1)求这个函数解析式
(2)设关于x的方程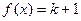 在[0,8]内有两个不同根
在[0,8]内有两个不同根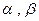 ,求
,求 的值及k的取值范围。
的值及k的取值范围。