下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.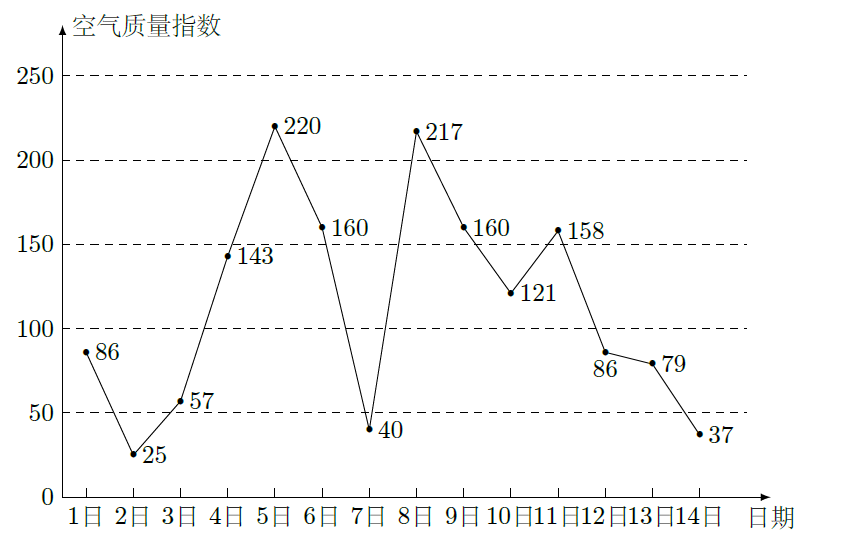
(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
已知函数
(Ⅰ)求
的最小正周期及最大值;
(Ⅱ)若
,且
,求
的值.
已知函数
(
为自然对数的底数)
(Ⅰ)若曲线
在点
处的切线平行于
轴,求
的值;
(Ⅱ)求函数
的极值;
(Ⅲ)当
时,若直线
与曲线
没有公共点,求
的最大值.
如图,在等腰直角
中,
,
,点
在线段
上.
(Ⅰ) 若
,求
的长;
(Ⅱ)若点
在线段
上,且
,问:当
取何值时,
的面积最小?并求出面积的最小值.
如图,抛物线
的焦点为
,准线
与
轴的交点为
.点
在抛物线
上,以
为圆心,
为半径作圆,设圆
与准线
交于不同的两点
,
.
(I)若点
的纵坐标为2,求
;
(II)若
,求圆
的半径.