已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.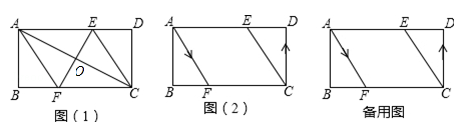
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
(自贡)在▱ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.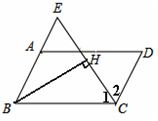
(内江)(本小题满分9分)如图,将▱ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.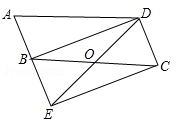
(内江)如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当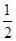 CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.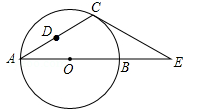
(南充)如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,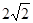 ,
,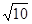 ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.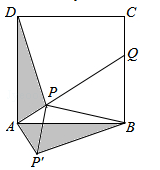
(成都)(本小题满分10分)已知AC,EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90.
(1)如图①,当四边形ABCD和EFCG均为正方形时,连接BF.
i)求证:△CAE∽△CBF;
ii)若BE=1,AE=2,求CE的长;
(2)如图②,当四边形ABCD和EFCG均为矩形,且 时,若BE=1,AE=2,CE=3,求k的值;
时,若BE=1,AE=2,CE=3,求k的值;
(3)如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)