(本小题满分10分)选修4-1:平面几何证明选讲
如图,在 中,
中, ,以
,以 为直径的⊙
为直径的⊙ 交
交 于
于 ,过点
,过点 作⊙
作⊙ 的切线交
的切线交 于
于 ,
, 交⊙
交⊙ 于点
于点 .
.
(Ⅰ)证明: 是
是 的中点;
的中点;
(Ⅱ)证明: .
.
某校从参加高一年级期末考试的学生中抽出60名学生,将其
成绩(均为整数)分成六段 ,
, …
… 后画出如下部分频率分布直方图.
后画出如下部分频率分布直方图.
观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
在△ABC中,sinB+sinC=sin(A-C).
(1)求A的大小;
(2)若BC=3,求△ABC的周长l的最大值.
某工厂对某产品的产量与成本的资料分析后有如下数据:
(1) 画出散点图。
(2) 求成本y与产量x之间的线性回归方程。(结果保留两位小数)
下面是计算应纳税所得额的算法过程,其算法如下:
第一步输入工资x(注x<=5000);
第二步如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);否则 y=25+0.1(x-1300)
第三步输出税款y, 结束。
请写出该算法的程序框图和程序。(注意:程序框图与程序必须对应)
(本小题满分14分)已知向量a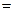
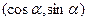 ,b
,b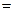
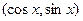 ,
,
c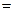

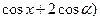 ,其中
,其中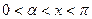 .
.
(1)若 ,求函数
,求函数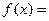 b·c的最小值及相应的
b·c的最小值及相应的 的值;
的值;
(2)若a与b的夹角为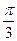 ,且a⊥c,求
,且a⊥c,求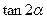 的值.
的值.