(本大题满分10分)选修4-5:不等式选讲
设函数
(Ⅰ)解不等式 ;
;
(Ⅱ)当 ,
, 时,证明:
时,证明: .
.
已知等差数列{ }的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
}的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设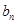 =
= ,求数列{
,求数列{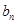 }的前n项和
}的前n项和 .
.
(设函数f(x)=|x+a|-|x-4|,x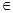 R
R
(1)当a=1时,解不等式f(x)<2;
(2)若关于x的不等式f(x)≤5-|a+l|恒成立,求实数a的取值范围.
在直角坐标系xoy中,曲线C1的参数方程为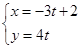 (t为参数),P为C1上的动点,Q为线段OP的中点.
(t为参数),P为C1上的动点,Q为线段OP的中点.
(1)求点Q的轨迹C2的方程;
(2)在以O为极点,x轴的正半轴为极轴(两坐标系取相同的长度单位)的极坐标系中,N为曲线p=2sinθ上的动点,M为C2与x轴的交点,求|MN|的最大值.
二阶矩阵M对应的变换将点(1,一1)与(-2,1)分别变换成点(-1,一1)与(0,一2).
①求矩阵M;
②设直线l在变换M的作用下得到了直线m:x-y=4,求l的方程.
已知函数f(x)=x2,g(x)=2elnx(x>0)(e为自然对数的底数).
(1)求F(x)=f(x)-g(x)(x>0)的单调区间及最小值;
(2)是否存在一次函数y=kx+b(k,b R),使得f(x)≥kx十b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.
R),使得f(x)≥kx十b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.