某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如表.
| |
优秀 |
非优秀 |
总计 |
| 课改班 |
|
50 |
|
| 非课改班 |
20 |
|
110 |
| 合计 |
|
|
210 |
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与课改有关”;
(2)把全部210人进行编号,从编号中有放回抽取4次,每次抽取1个,记被抽取的4人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望Eξ.
(本小题满分10分)
已知函数 的定义域为A,函数
的定义域为A,函数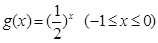 的值域为B.
的值域为B.
(I)求 ;
;
(II)若 ,且
,且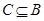 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知函数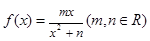 在
在 处取得极值
处取得极值 .
.
⑴求 的解析式;
的解析式;
⑵设 是曲线
是曲线 上除原点
上除原点 外的任意一点,过
外的任意一点,过 的中点且垂直于
的中点且垂直于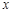 轴的直线交曲线于点
轴的直线交曲线于点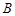 ,试问:是否存在这样的点
,试问:是否存在这样的点 ,使得曲线在点
,使得曲线在点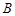 处的切线与
处的切线与 平行?若存在,求出点
平行?若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
⑶设函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求
,求
实数 的取值范围.
的取值范围.
(本小题满分14分)已知定义域为R的函数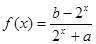 是奇函数.
是奇函数.
(1)求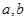 的值;
的值;
(2)用定义证明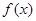 在
在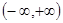
 上为减函数.
上为减函数.
(3)若对于任意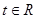 ,不等式
,不等式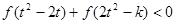 恒成立,求
恒成立,求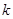 的范围.
的范围.
(本小题满分14分)某种商品的成本为5元/ 件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元每天销售量就减少10件;而降价后,日销售量Q(件)与实际销售价x(元)满足关系:
|
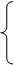
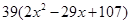
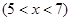 [
[

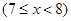 [
[
(本小题满分14分)已知函数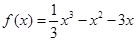 在
在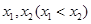 处取得极值,记点
处取得极值,记点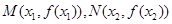 .
.
⑴求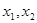 的值;
的值;
⑵证明:线段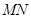 与曲线
与曲线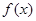 存在异于
存在异于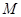 、
、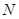 的公共点;
的公共点;