某校乒乓球队有3名男同学A，B，C和3名女同学X，Y，Z，其年级情况如下表：
| |
一年级 |
二年级 |
三年级 |
| 男同学 |
A |
B |
C |
| 女同学 |
X |
Y |
Z |
现从这6名同学中随机选出2人参加乒乓球比赛（每人被选到的可能性相同）．
（1）用表中字母列举出所有可能的结果；
（2）设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件M发生的概率．
如图所示,矩形ABCD中,AB=a,AD=b,过点D作DE⊥AC于E,交直线AB于F.现将△ACD沿对角线AC折起到△PAC的位置,使二面角P
ACB的大小为60°.过P作PH⊥EF于H.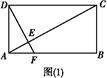
(1)求证:PH⊥平面ABC;
(2)若a+b=2,求四面体P
ABC体积的最大值.
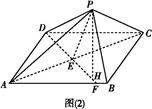
如图(1)所示,△ABC是等腰直角三角形,AC=BC=4,E、F分别为AC、AB的中点,将△AEF沿EF折起,使A′在平面BCEF上的射影O恰为EC的中点,得到图(2).
(1)求证:EF⊥A′C;
(2)求三棱锥F
A′BC的体积.
如图所示,直三棱柱ABC
A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2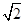
,求三棱锥CA1DE的体积.
如图,三棱柱ABC
A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=
,求三棱柱ABCA1B1C1的体积.
如图,四棱锥P
ABCD中,PA⊥底面ABCD,PA=2
,BC="CD=2," ∠ACB=∠ACD=
.
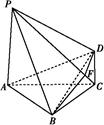
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥PBDF的体积.