从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
| 质量指标 值分组 |
[75,85) |
[85,95) |
[95,105) |
[105,115) |
[115,125) |
| 频数 |
6 |
26 |
38 |
22 |
8 |
(Ⅰ)在答题卡上列出这些数据频率分布表,并作出频率分布直方图;
(Ⅱ)估计这种产品质量指标值的平均值及方差(同一组中的数据用该组区间的中点值作代表).
三棱柱 中,侧棱与底面垂直,
中,侧棱与底面垂直,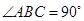 ,
,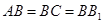 ,
, 是
是 的中点,
的中点,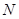 是
是 与
与 的交点.
的交点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: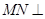 平面
平面 .
.
已知直线 ,
,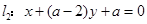 .
.
(Ⅰ)若 ,求实数
,求实数 的值;
的值;
(Ⅱ)当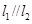 时,求直线
时,求直线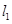 与
与 之间的距离.
之间的距离.
如图,正方体 的棱长为
的棱长为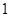 ,线段
,线段 上有两个动点
上有两个动点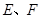 ,且
,且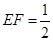 ,则下列结论中错误的是()
,则下列结论中错误的是()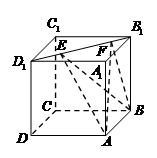
A. |
B.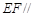 平面 平面 |
C.三棱锥 的体积为定值 的体积为定值 |
D. 的面积与 的面积与 的面积相等 的面积相等 |
已知函数 ,
, .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)设 ,若对任意的两个实数
,若对任意的两个实数 满足
满足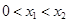 ,总存在
,总存在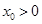 ,使得
,使得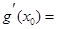
 成立,证明:
成立,证明: .
.
已知椭圆C: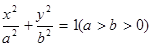 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,点G在椭圆C上,且
,点G在椭圆C上,且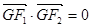 ,
,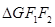 的面积为3.
的面积为3.
(1)求椭圆C的方程:
(2)设椭圆的左、右顶点为A,B,过 的直线
的直线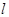 与椭圆交于不同的两点M,N(不同于点A,B),探索直线AM,BN的交点能否在一条垂直于
与椭圆交于不同的两点M,N(不同于点A,B),探索直线AM,BN的交点能否在一条垂直于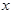 轴的定直线上,若能,求出这条定直线的方程;若不能,请说明理由。
轴的定直线上,若能,求出这条定直线的方程;若不能,请说明理由。