甲、乙两人在罚球线投球命中的概率分别为 与
与 ,且各次投球相互之间没有影响.
,且各次投球相互之间没有影响.
(1)甲、乙两人在罚球线各投球一次,求这二次投球中恰好命中一次的概率;
(2)甲、乙两人在罚球线各投球二次,求这四次投球中至少有一次命中的概率.
已知关于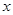 的不等式
的不等式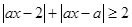
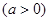 .
.
(1)当 时,求此不等式的解集;(2)若此不等式的解集为R,求实数
时,求此不等式的解集;(2)若此不等式的解集为R,求实数 的取值范围.
的取值范围.
已知圆x2+y2-2ax-6ay+10a2-4a=0(0<a 4)的圆心为C,直线L: y=x+m。
4)的圆心为C,直线L: y=x+m。
(1)若a=2,求直线L被圆C所截得的弦长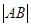 的最大值;
的最大值;
(2)若m=2,求直线L被圆C所截得的弦长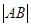 的最大值;
的最大值;
已知点P(-2,-3),圆C: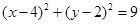 ,过P点作圆C的两条切线,切点分别为A、B
,过P点作圆C的两条切线,切点分别为A、B
(1)求过P、A、B三点的外接圆的方程;
(2)求直线AB的方程.
在等差数列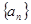 中,
中,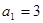 ,其前
,其前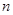 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数,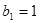 ,公比为
,公比为 ,且
,且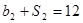 ,
, .
.
(1)求 与
与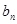 ;(2)设数列
;(2)设数列 满足
满足 ,求
,求 的前
的前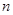 项和
项和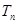 .
.
已知圆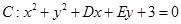 关于直线
关于直线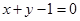 对称,圆心
对称,圆心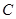 在第二象限,半径为
在第二象限,半径为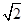 .
.
(1)求圆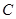 的方程;
的方程;
(2)是否存在直线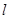 与圆
与圆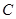 相切,且在
相切,且在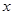 轴、
轴、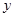 轴上的截距相等?若存在,求直线的方程;若不存在,说明理由.
轴上的截距相等?若存在,求直线的方程;若不存在,说明理由.