某商场的销售部经过市场调查发现,该商场的某种商品每日的销售量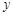 (单位:千克)与销售价格
(单位:千克)与销售价格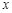 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式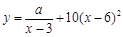 ,其中
,其中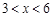 ,
, 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(Ⅰ)求 的值;
的值;
(Ⅱ)若该商品的成本为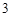 元/千克,试确定销售价格
元/千克,试确定销售价格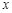 的值,使该商场每日销售该商品所获得的利润最大.
的值,使该商场每日销售该商品所获得的利润最大.
如图,等边三角形
的边长为
,且其三个顶点均在抛物线
上。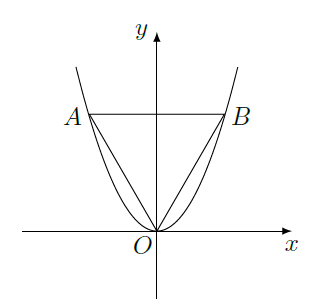
(1)求抛物线
的方程;
(2)设动直线
与抛物线
相切于点
,与直线
相交于点
,证明以
为直径的圆恒过
轴上某定点.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)
(2)
(3)
(4)
(5)
(Ⅰ)试从上述五个式子中选择一个,求出这个常数
(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
如图,在长方体
中,
,
,
为棱
上的一点。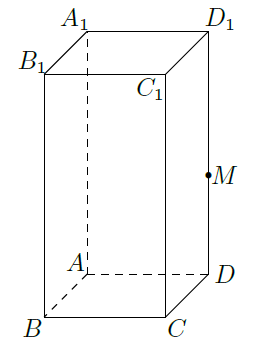
Ⅰ求三棱锥 的体积;
Ⅱ当 取得最小值时,求证: 平面 .
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
| 销量y(件) |
90 |
84 |
83 |
80 |
75 |
68 |
(I)求回归直线方程 ,其中 , ;
(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利 润,该产品的单价应定为多少元?(利润=销售收入-成本)
在等差数列 和等比数列 中, , , 的前10项和 .
(Ⅰ)求
和
;
(Ⅱ)现分别从
和
的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率