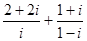(本小题12分)设函数
(1)把函数 的图像向右平移
的图像向右平移 个单位,再向下平移
个单位,再向下平移 个单位得到函数
个单位得到函数 的图像,求函数
的图像,求函数 在区间
在区间 上的最小值,并求出此时
上的最小值,并求出此时 的值;
的值;
(2)已知△ABC中,角A,B,C的对边分别为a,b,c.若 .求a的最小值.
.求a的最小值.
在某校对30名女生与80名男生进行是否有懒惰习惯进行调查,发现女生中有15人有懒惰习惯,男生中有50人有懒惰习惯。
(1)请根据上述数据填写2×2列联表;
| 懒惰 |
不懒惰 |
总计 |
|
| 女 |
|||
| 男 |
|||
| 总计 |
(2)能否判断懒惰是否与性别有关。(参考公式: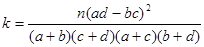 )
)
临界值表
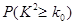 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
在 中,三个内角A、B、C的对边分别为a,b,c,且A、B、C成等差数列,a,b,c成等比数列,请用分析法证明:
中,三个内角A、B、C的对边分别为a,b,c,且A、B、C成等差数列,a,b,c成等比数列,请用分析法证明: 为等边三角形。
为等边三角形。
下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| X |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)(参考公式: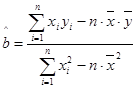 ,
, )
)
用反证法证明:若三个互不相等的正数, 成等差数列,求证:
成等差数列,求证: 不可能成等比数列。
不可能成等比数列。
计算:
(1)、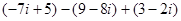 (2)、
(2)、
(3)、