甲市火车货运站现有苹果1530吨，梨1150吨，安排一列货车将这批苹果和梨运往乙市．这列货车可以挂A、B两种不同规格的货箱共50节，已知用一节A型货箱的运费是0.5万元，用一节B型货箱的运费用是.0.8万元．
（1）设运输这批苹果和梨的总运费为y（万元），用A型货箱的节数为x（节），试写出y与x的函数关系式．
（2）已知35吨苹果和15吨梨可装满一节A型货箱，25吨苹果和35吨梨可装满一节B型车箱，请问运输所有苹果和梨的方案共有几种，请设计出来．
（3）利用函数的性质说明，在第（2）问的方案中，哪种方案的运费最少，最少运费用是多少？
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：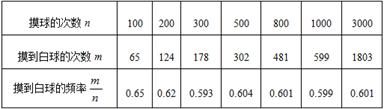
（1）请估计：当n很大时，摸到白球的频率将会接近 ；（精确到0．1）
（2）假如你摸一次，你摸到白球的概率P（白球）= ；
（3）试估算盒子里黑、白两种颜色的球各有多少只？
阅读材料并回答问题：（本题8分）
我们知道，乘法公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，如：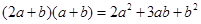
，就可以用图1或图2等图形的面积表示．
（1）请写出图3所表示的代数恒等式：；
（2）试画一个几何图形，使它的面积表示：
；
（3）请仿照上述方法另写一个含有
，
的代数恒等式，并画出与它对应的几何图形．
同学们已经体会到灵活运用乘法公式给整式乘法带来的方便，快捷．相信通过下面材料的学习探究，会使你大开眼界并获得成功的喜悦．
例：用简便方法计算195×205．
解：195×205
=（200-5）（200+5）①
=
②
=39975
（1）例题求解过程中，第②步变形是利用（填乘法公式的名称）．
（2）用简便方法计算：9×11×101×10001
基本事实：若
（a>0且a≠1，m、n是正整数），则m＝n．
试利用上述基本事实分别求下列各等式中x的值：
①
；②
．
（本题6分）AB⊥BC，∠1+∠2=90°，∠2=∠3．BE与DF平行吗？为什么？
解：BE∥DF．
∵AB⊥BC，
∴∠ABC=°，
即∠3+∠4=°．
又∵∠1+∠2=90°，
且∠2=∠3，
∴=．
理由是：________________．
∴BE∥DF．
理由是：________________．