先仔细阅读材料，再尝试解决问题：
完全平方公式x2±2xy+y2=（x±y）2及（x±y）2的值恒为非负数的特点在数学学习中有着广泛的应用，比如探求多项式2x2+12x﹣4的最大（小）值时，我们可以这样处理：
解：原式=2（x2+6x﹣2）
=2（x2+6x+9﹣9﹣2）
=2[（x+3）2﹣11]
=2（x+3）2﹣22
因为无论x取什么数，都有（x+3）2的值为非负数
所以（x+3）2的最小值为0，此时x=﹣3
进而2（x+3）2﹣22
的最小值是2×0﹣22=﹣22
所以当x=﹣3时，原多项式的最小值是﹣22
解决问题：
请根据上面的解题思路，探求多项式3x2﹣6x+12的最小值是多少，并写出对应的x的取值．
解方程：
计算：（1）
；（2）
已知：如图①，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t(s)（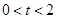
），解答下列问题：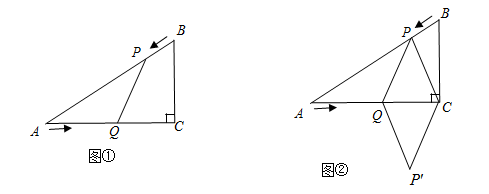
（1）当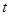
为何值时，PQ∥BC？
（2）设△AQP的面积为y（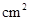
），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；
（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻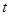，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．
如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A．与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．
（1）试判断BC所在直线与小圆的位置关系，并说明理由；
（2）试判断线段AC、AD、BC之间的数量关系，并说明理由；
（3）若AB=8cm，BC=10cm，求大圆与小圆围成的圆环的面积．（结果保留π）
某超市销售一批羽绒服，平均每天可售了20件，每件盈利40元，为扩大销售增加盈利，超市决定适当降价，如果每件羽绒服降阶5元，平均每天可多售出10件，如果超市要保证平均每天要盈利1200元，同时又要顾客得到实惠，那么每件羽绒服应降价多少元？