遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位: 的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.
课外劳动时间频数分布表:
|
劳动时间分组 |
频数 |
频率 |
|
|
2 |
0.1 |
|
|
4 |
|
|
|
6 |
0.3 |
|
|
|
0.25 |
|
|
3 |
0.15 |
解答下列问题:
(1)频数分布表中 , ;将频数分布直方图补充完整;
(2)若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于 的人数;
(3)已知课外劳动时间在 的男生人数为2人,其余为女生,现从该组中任选2人代表学校参加"全市中学生劳动体验"演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.

如图, 是 的直径,点 是 上一点, 的平分线 交 于点 ,过点 作 交 的延长线于点 .
(1)求证: 是 的切线;
(2)过点 作 于点 ,连接 .若 , ,求 的长度.

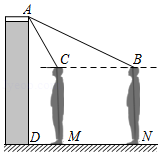
某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门 的顶部 处距地面高为 ,为了解自己的有效测温区间.身高 的小聪做了如下实验:当他在地面 处时测温门开始显示额头温度,此时在额头 处测得 的仰角为 ;在地面 处时,测温门停止显示额头温度,此时在额头 处测得 的仰角为 .求小聪在地面的有效测温区间 的长度.(额头到地面的距离以身高计,计算精确到 , , ,
如图,已知抛物线 经过两点 , , 是抛物线与 轴的交点.
(1)求抛物线的解析式;
(2)点 在平面直角坐标系第一象限内的抛物线上运动,设 的面积为 ,求 关于 的函数表达式(指出自变量 的取值范围)和 的最大值;
(3)点 在抛物线上运动,点 在 轴上运动,是否存在点 、点 使得 ,且 与 相似,如果存在,请求出点 和点 的坐标.

如图, 是 的直径, 为 上一点,连接 , 于点 , 是直径 延长线上一点,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
