(本小题满分12分)
已知函数
(I)当1<a <4时,函数 在[2,4]上的最小值为
在[2,4]上的最小值为 ,求a;
,求a;
(Ⅱ)若存在x0∈(2,+∞),使得 <0,求a的取值范围.
<0,求a的取值范围.
已知抛物线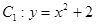 与圆
与圆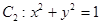
(I)求抛物线 上一点
上一点 与圆
与圆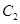 上一动点
上一动点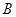 的距离的最小值;
的距离的最小值;
(II)将圆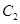 向上平移
向上平移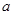 个单位后能否使圆
个单位后能否使圆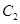 在抛物线
在抛物线 内并触及抛物线
内并触及抛物线 (与
(与 相切于顶点)的底部?若能,请求出
相切于顶点)的底部?若能,请求出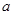 的值,若不能,试说明理由;
的值,若不能,试说明理由;
(III)设点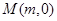 为
为 轴上一个动点,过
轴上一个动点,过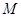 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为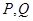 ,求证:直线
,求证:直线 过定点,并求出定点坐标。
过定点,并求出定点坐标。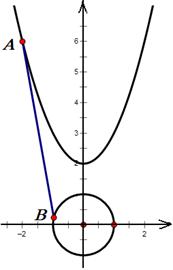
如图,直四棱柱 中,底面
中,底面 是
是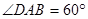 的菱形,
的菱形, ,
, ,点
,点 在棱
在棱 上,点
上,点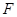 是棱
是棱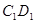 的中点;
的中点;
(I)若 是
是 的中点,求证:
的中点,求证: ;
;
(II)求出 的长度,使得
的长度,使得 为直二面角。
为直二面角。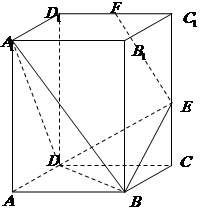
设数列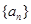 的前n项和为
的前n项和为 ,且
,且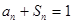 (I)求数列
(I)求数列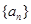 的通项公式;
的通项公式;
(II)设数列 满足:
满足: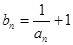 ,又
,又 ,且数列
,且数列 的前n项和为
的前n项和为 ,求证:
,求证: 。
。
已知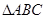 的三内角A,B,C所对三边分别为a,b,c,且
的三内角A,B,C所对三边分别为a,b,c,且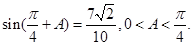 (I)求
(I)求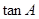 的值。(II)若
的值。(II)若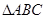 的面积
的面积 求a的值。
求a的值。
设 为整数,集合
为整数,集合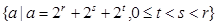 中的数由小到大组成数列
中的数由小到大组成数列 .(1)写出数列
.(1)写出数列 的前三项;(2)求
的前三项;(2)求 .
.