(本小题12分) 已知定圆
 ,定直线
,定直线
 ,过
,过 的一条动直线
的一条动直线 与直线相交于
与直线相交于 ,与圆
,与圆 相交于
相交于 两点,
两点,
(1)当 与
与 垂直时,求出
垂直时,求出 点的坐标,并证明:
点的坐标,并证明: 过圆心
过圆心 ;
;
(2)当 时,求直线
时,求直线 的方程.
的方程.
某种产品的广告费支出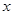 (单位:万元)与销售额
(单位:万元)与销售额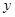 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
广告费支出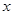 |
2 |
4 |
5 |
6 |
8 |
销售额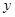 |
30 |
40 |
60 |
50 |
70 |
(1)计算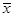 ,
,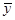 的值并求点
的值并求点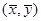 对应的复数
对应的复数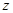 ;
;
(2)完成下表并求回归直线方程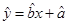 。
。
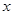 |
2 |
4 |
5 |
6 |
8 |
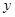 |
30 |
40 |
60 |
50 |
70 |
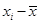 |
|||||
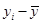 |
|||||
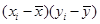 |
|||||
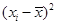 |
( 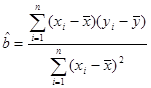 )
)
已知函数f(x)=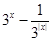 .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若 恒成立,求m的取值范围。
恒成立,求m的取值范围。
已知圆C:x2-4x+y2+2y-3=0内有一点P(1,1),AB为过点P且倾斜角为 的弦。
的弦。
(1)当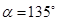 时,求AB的长度;
时,求AB的长度;
(2)求弦AB的最小值,并写出此时的直线方程。
如图,在四棱锥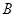 中,底面
中,底面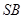 是直角梯形,
是直角梯形,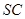 ∥
∥ ,
, ,
,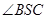 ⊥平面SAD,点
⊥平面SAD,点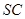 是
是 的中点,且
的中点,且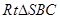 ,
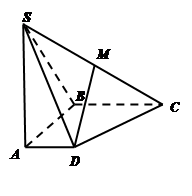
,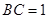 .
. 
(1)求四棱锥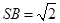 的体积;
的体积;
(2)求证: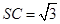 ∥平面
∥平面 ;
;
(3)求直线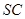 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.
2013年春运期间,长沙火车站在某大学开设了一个服务窗口。假设每一位顾客办理业务所需时间都是整数分钟,对这1000名顾客办理业务所需时间统计结果如下:
| 办理业务所需时间(分钟) |
1 |
2 |
3 |
4 |
5 |
| 人数 |
100 |
400 |
300 |
100 |
100 |
以记录的这1000名顾客办理业务所需时间的频率作为各所需时间发生的概率。
(1)求一位顾客办理业务时间不超过3分钟的概率;
(2)估计顾客办理业务所需时间的平均值。