如图，已知ABCD的周长为8cm，∠B30°，若边长AB为-优题课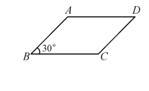

如图，已知ABCD的周长为8 cm，∠B=30°，若边长AB为x cm．

（1）写出平行四边形ABCD的面积y（cm²）与x（cm）的函数关系式，并求自变量x的取值范围．
（2）当x取什么值时，y的值最大？并求出最大值．

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

如图， $AB$ 为 $⊙ O$ 的直径，射线 $AD$ 交 $⊙ O$ 于点 $F$ ，点 $C$ 为劣弧 $\hat{BF}$ 的中点，过点 $C$ 作 $CE ⊥ AD$ ，垂足为 $E$ ，连接 $AC$ ．

（1）求证： $CE$ 是 $⊙ O$ 的切线；

（2）若 $∠ BAC = 30 °$ ， $AB = 4$ ，求阴影部分的面积．

在4月23日“世界读书日”来临之际，某校为了了解学生的课外阅读情况，从全校随机抽取了部分学生，调查了他们平均每周的课外阅读时间 $t$ （单位：小时）．把调查结果分为四档， $A$ 档： $t < 8$ ； $B$ 档： $8 ⩽ t < 9$ ； $C$ 档： $9 ⩽ t < 10$ ； $D$ 档： $t ⩾ 10$ ．根据调查情况，给出了部分数据信息：

① $A$ 档和 $D$ 档的所有数据是：7，7，7.5，10，7，10，7，7.5，7，7，10.5，10.5；

②图1和图2是两幅不完整的统计图．

根据以上信息解答问题：

（1）求本次调查的学生人数，并将图2补充完整；

（2）已知全校共1200名学生，请你估计全校 $B$ 档的人数；

（3）学校要从 $D$ 档的4名学生中随机抽取2名作读书经验分享，已知这4名学生1名来自七年级，1名来自八年级，2名来自九年级，请用列表或画树状图的方法，求抽到的2名学生来自不同年级的概率．

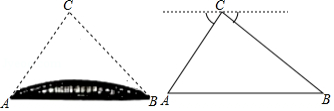
某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度．如图，桥 $AB$ 是水平并且笔直的，测量过程中，小组成员遥控无人机飞到桥 $AB$ 的上方120米的点 $C$ 处悬停，此时测得桥两端 $A$ ， $B$ 两点的俯角分别为 $60 °$ 和 $45 °$ ，求桥 $AB$ 的长度．

先化简，再求值： $(1 - \frac{x + 1}{x^{2} - 2 x + 1}) \div \frac{x - 3}{x - 1}$ ，其中 $x$ 是16的算术平方根．

发现规律

（1）如图①， $ΔABC$ 与 $ΔADE$ 都是等边三角形，直线 $BD$ ， $CE$ 交于点 $F$ ．直线 $BD$ ， $AC$ 交于点 $H$ ．求 $∠ BFC$ 的度数．

（2）已知： $ΔABC$ 与 $ΔADE$ 的位置如图②所示，直线 $BD$ ， $CE$ 交于点 $F$ ．直线 $BD$ ， $AC$ 交于点 $H$ ．若 $∠ ABC = ∠ ADE = α$ ， $∠ ACB = ∠ AED = β$ ，求 $∠ BFC$ 的度数．

应用结论

（3）如图③，在平面直角坐标系中，点 $O$ 的坐标为 $(0, 0)$ ，点 $M$ 的坐标为 $(3, 0)$ ， $N$ 为 $y$ 轴上一动点，连接 $MN$ ．将线段 $MN$ 绕点 $M$ 逆时针旋转 $60 °$ 得到线段 $MK$ ，连接 $NK$ ， $OK$ ．求线段 $OK$ 长度的最小值．