(本小题满分10分)在直角坐标系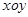 中,直线
中,直线 经过点
经过点 (-1,0),其倾斜角为
(-1,0),其倾斜角为 ,以原点
,以原点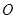 为极点,以
为极点,以 轴非负半轴为极轴,与直角坐标系
轴非负半轴为极轴,与直角坐标系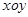 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线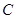 的极坐标方程为
的极坐标方程为
(1)若直线 与曲线
与曲线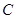 有公共点,求
有公共点,求 的取值范围;
的取值范围;
(2)设 为曲线
为曲线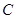 上任意一点,求
上任意一点,求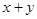 的取值范围
的取值范围
设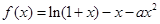 .
.
(1)当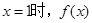 取到极值,求
取到极值,求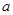 的值;
的值;
(2)当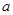 满足什么条件时,
满足什么条件时,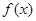 在区间
在区间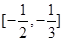 上有单调递增的区间.
上有单调递增的区间.
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格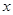 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式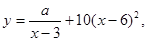 其中
其中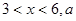 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求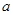 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格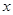 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
已知各项均为正数的数列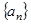 前n项和为
前n项和为 ,首项为
,首项为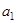 ,且
,且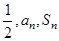 等差数列。
等差数列。
(1)求数列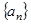 的通项公式;
的通项公式;
(2)若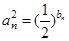 ,设
,设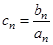 ,求数列
,求数列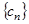 的前n项和
的前n项和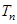 .
.
设函数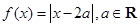 .
.
(1)若不等式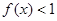 的解集为
的解集为 ,求
,求 的值;
的值;
(2)若存在 ,使
,使 ,求
,求 的取值范围.
的取值范围.
已知直线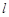 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,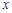 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)若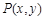 是直线
是直线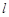 与圆面
与圆面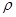 ≤
≤ 的公共点,求
的公共点,求 的取值范围.
的取值范围.