已知函数 .
.
(1)若曲线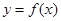 在
在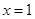 处的切线的方程为
处的切线的方程为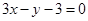 ,求实数a、b的值;
,求实数a、b的值;
(2)若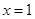 是函数
是函数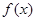 的极值点,求实数a的值;
的极值点,求实数a的值;
(3)若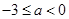 ,且对任意
,且对任意 ,都有
,都有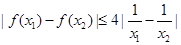 ,求实数t的取值范围.
,求实数t的取值范围.
(1)已知n∈N*,求证:1+2+22+23+…+25n-1能被31整除;
(2)求0.9986的近似值,使误差小于0.001.
有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,共有多少种不同排法?
已知平面 ∥
∥ ,在
,在 内有4个点,在
内有4个点,在 内有6个点.
内有6个点.
(1)过这10个点中的3点作一平面,最多可作多少个不同平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)上述三棱锥中最多可以有多少个不同的体积?
课外活动小组共13人,其中男生8人,女生5人,并且男、女各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有一名女生;
(2)两队长当选;
(3)至少有一名队长当选;
(4)至多有两名女生当选.
有6本不同的书按下列分配方式分配,问共有多少种不同的分配方式?
(1)分成1本、2本、3本三组;
(2)分给甲、乙、丙三人,其中一人1本,一人2本,一人3本;
(3)分成每组都是2本的三组;
(4)分给甲、乙、丙三人,每人2本.